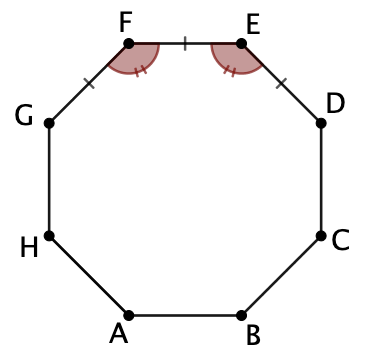
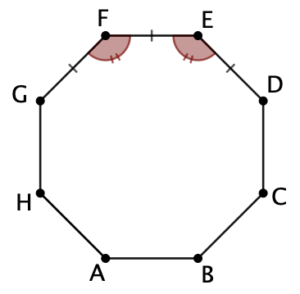
Un octogone régulier est un polygone formé de huit côtés de même longueur et de huit angles internes de même mesure.
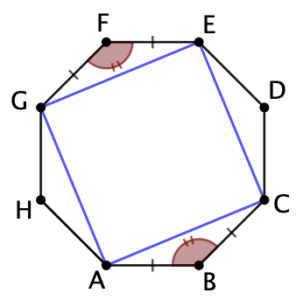ACEG est un carré
Les triangles isocèles GFE et ABC sont isométriques car ils ont la même mesure d’angle entre leurs deux côtés de même longueur. Par conséquent GE = AC.
On démontre de la même façon que CE = AG. Première conclusion : ACEG est un losange.
Étant donné, d’une part que les quatre triangles ABC, CDE, EFG et GHA sont isométriques, d’autre part que les huit angles intérieurs sont de même mesure, il vient que les quatre angles du losange ACEG sont de même mesure, donc égaux à 90°. Conclusion : ACEG est un carré.
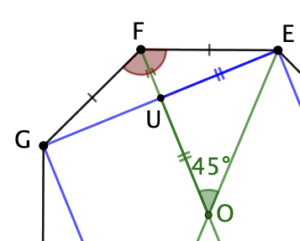L’angle au centre de l’octogone mesure 45°
FG = FE donc F appartient à la médiatrice de [GE]. Les médiatrices et les diagonales d’un carré sont concourantes en O. Dans un carré une médiatrice et un diagonale voisines forment entre elles un angle de 45°. Donc les huit angles au centre de l’octogone mesurent 45°.
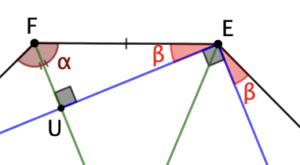L’angle intérieur mesure 135°
On a les deux égalités suivantes : 
et 
.
Une résolution évidente donne : 
et 
.
Un calcul élémentaire permet de constater que les deux angles 
, donc que OFE est isocèle en O. Par conséquent OE = OF.
