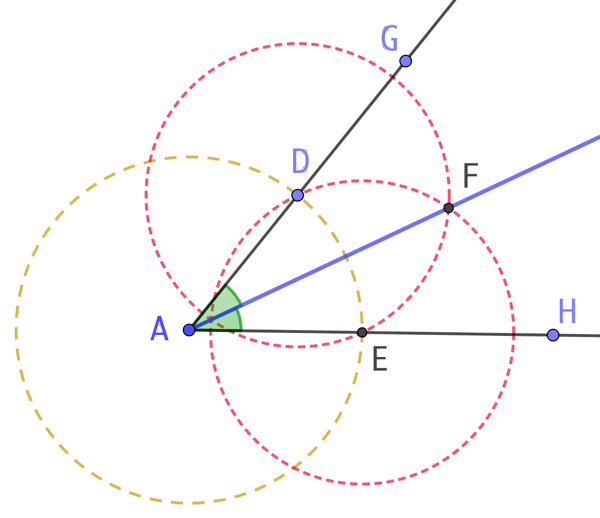
 Soit un angle HAG de sommet A. On construit la bissectrice de cet angle ainsi :
Soit un angle HAG de sommet A. On construit la bissectrice de cet angle ainsi :
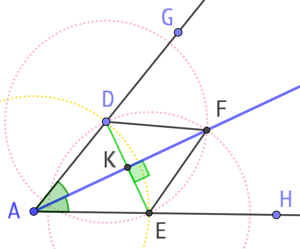
- On place un point D sur la demi-droite [AG). Cela pourrait être aussi le point G.
- On trace le cercle de centre A passant par D. Ce cercle coupe la demi-droite [AH) au point E.
- On trace deux cercles de même rayon, de centre D et E. On choisit le rayon de manière à ce que ces deux cercles se croisent.
- Soit F l’un des points d’intersection de ces deux cercles. La demi-droite [AF) est la bissectrice de l’angle
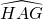 . C’est à dire que les angles
. C’est à dire que les angles 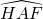 et
et 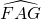 (en vert sur la figure) ont la même mesure.
(en vert sur la figure) ont la même mesure.
Explications :
Les points D et E appartiennent au cercle de centre A, donc les distances AD et AE sont égales. Par conséquent A appartient à la médiatrice du segment [DE]. Cette médiatrice est aussi la bissectrice que nous cherchons car :
- on considère le point K, intersection de [DE] et de la médiatrice de [DE];
- les deux triangles ADK et AEK sont isométriques. En effet :
- on sait déjà que
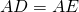 ;
; - AK est un côté commun au deux triangles ;
- K est le milieu de [DE] car sur la médiatrice de [DE], donc
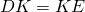 .
.
- on sait déjà que
- par conséquent ces deux triangles ont aussi les mêmes mesures d’angles. Donc les angles
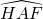 et
et 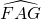 sont de même mesure.
sont de même mesure.
Pour tracer cette médiatrice, il suffit de trouver un autre point appartenant à cette médiatrice. Ce sera le point F, intersection des deux cercles.
Remarque : On vient de démontrer au passage que dans un triangle isocèle, la médiatrice et la bissectrice issues du sommet sont confondues. On pourrait d’ailleurs ajouter que la hauteur et la médiane issues de ce même sommet sont confondues avec les deux autres droites.
Remarque : Il s’agit de la proposition I.9 des Éléments d’Euclide à laquelle on peut ajouter la proposition I.10 qui présente la méthode pour couper un segment en deux parties de même longueur.
