On construit un carré dont l’un des côtés AB est donné ainsi :
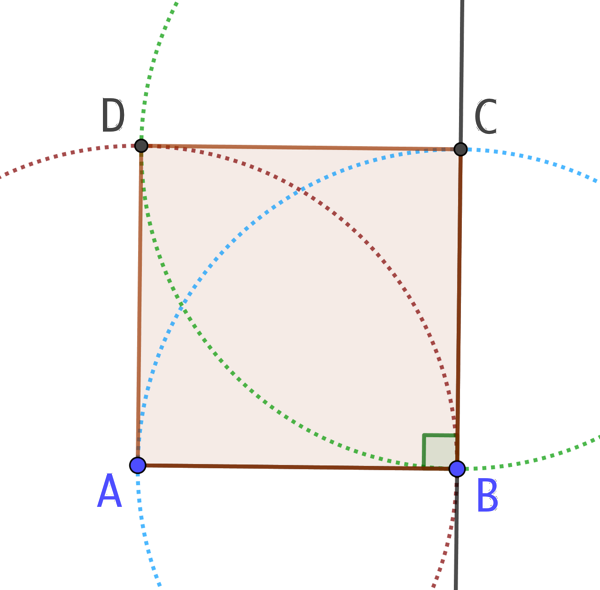
- On trace la perpendiculaire à (AB) passant par B.
- On trace le cercle de centre B et passant par A. Ce cercle coupe la perpendiculaire au point C.
- On trace les deux cercles de centre A passant par B et le cercle de centre C passant par B. Ces deux cercles se croisent en deux points dont le point D. Le quadrilatère ABCD est un carré.
Explications :
De par sa construction, le point D vérifie les égalités de longueurs : AD = AB et CD = CB. Or de par sa construction, le point C vérifie l’égalité de longueur : BC = BA. On en conclut que les quatre côtés du quadrilatère ABCD ont la même longueur. ABCD est donc un losange. Comme (AB) et (BC) sont perpendiculaires, ABCD est un losange possédant un angle droit, c’est donc un carré.
Pour construire un rectangle, il suffit d’appliquer le même protocole en modifiant l’écartement du compas en fonction de sa longueur et de sa largeur.
Remarque : Il s’agit de la proposition I.46 des Éléments d’Euclide. Les étapes de constructions proposées par Euclide sont légèrement différentes.
