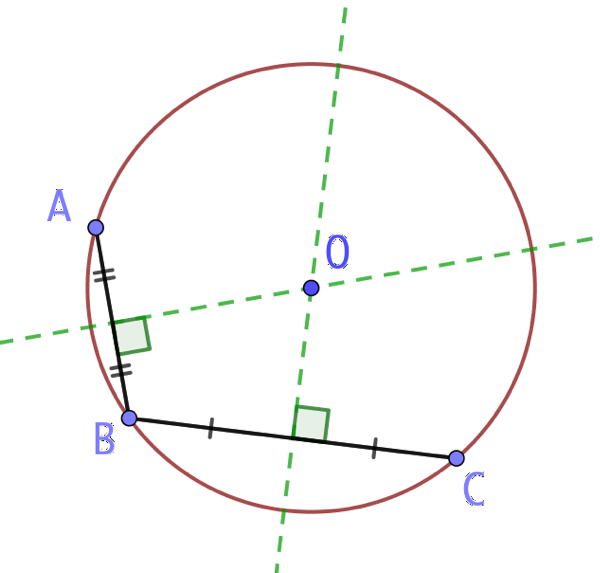
 L’objectif est de retrouver la position du centre d’un cercle donné. On procède ainsi :
L’objectif est de retrouver la position du centre d’un cercle donné. On procède ainsi :
- On place trois points A, B et C quelconques sur le cercle.
- On trace les segments AB et BC.
- On trace leur médiatrice. L’intersection de ces deux médiatrices est le centre du cercle qu’il fallait retrouver.
Explications :
Le cercle est par définition le lieu de tous les points équidistants d’un point particulier que l’on appelle le centre de ce cercle. A et B appartiennent à ce cercle donc sont équidistants du centre du cercle. On peut aussi énoncer que le point O est équidistant des points A et B, donc O appartient à la médiatrice du segment [AB].
On démontre de la même manière que O appartient à la médiatrice du segment [BC]. O est donc le point d’intersection de ces deux médiatrices.
Remarque : Ce résultat s’inspire de la proposition III.9 des Éléments d’Euclide.
