L’objectif est de retrouver la position du centre d’un cercle donné. On procède ainsi :
- On place deux points quelconques B et C sur le cercle.
- On trace le segment [BC] puis les deux perpendiculaires à [BC] passant par B et C. Ces deux droites coupent le cercle aux points A et D.
- On trace les segments [AC] et [BD] qui se croisent au centre du cercle recherché.
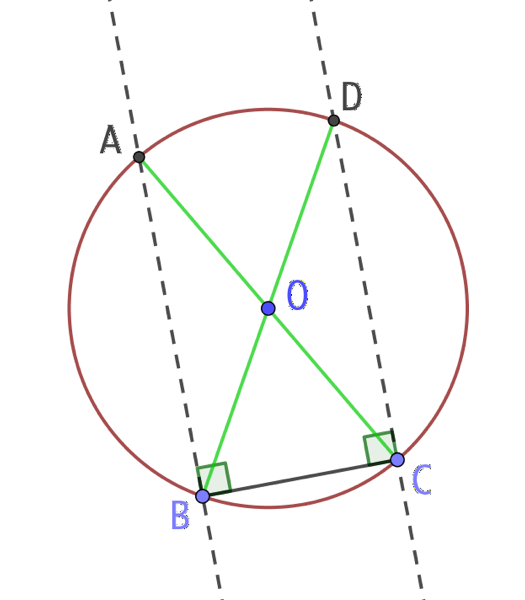
Explications :
Le triangle ABC est rectangle en B et inscrit dans le cercle. Par conséquent l’hypoténuse [AC] de ce triangle est un diamètre du cercle.
Le triangle BCD est rectangle en C et inscrit dans le cercle. Par conséquent l’hypoténuse [BD] de ce triangle est un diamètre du cercle. Les deux hypoténuses étant des diamètres du cercle, elles se croisent nécessairement au centre O de ce cercle.
