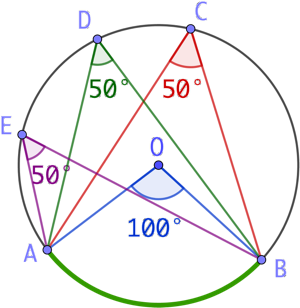
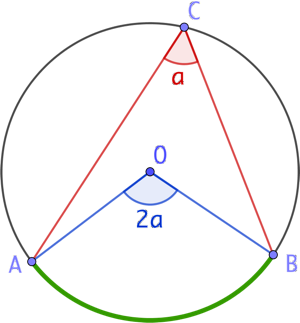
On construit l’angle au centre et l’angle inscrit dans un cercle de centre O ainsi :
- On choisit trois points quelconques du cercle : A, B et C. On trace l’angle
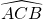, c’est un angle inscrit. - On trace l’angle
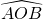, c’est un angle au centre dont la mesure représente le double de celle de l’angle au inscrit 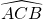. On dit que les deux angles interceptent le même arc de cercle AB.
Explications :
On cherche à démontrer que 
.
On observe que les triangles OAC, OBC et OAB sont isocèles et donc que leurs angles à la base ont la même mesures.
On considère le triangle ABC. La somme de des mesures de ses trois angles fait 
, soit l’égalité : 
que l’on peut simplifier en 
. Comme 
, l’égalité devient 
d’où la valeur de 
.
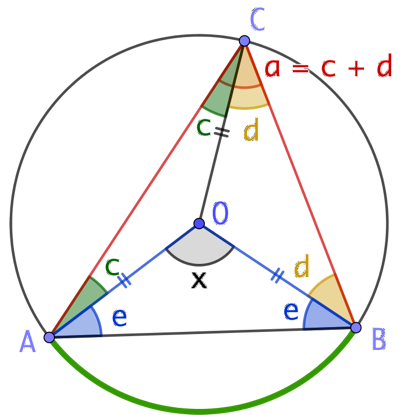On considère à présent le triangle OAB et on écrit que la somme des mesures de ses trois angles fait , soit l’égalité : 
. Donc 
. L’angle au centre a donc une mesure égale à deux fois celle de l’angle inscrit interceptant le même arc de cercle.
Conséquence :
Tous les angles inscrits interceptant le même arc de cercle ont la même mesure.
Remarque : Il s’agit de la proposition III.21 des Éléments d’Euclide.
