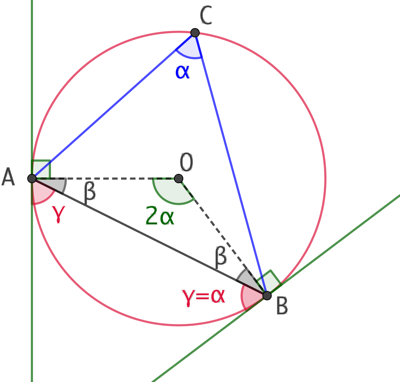
Étant donnés trois points A, B et C d’un cercle de centre O, la corde [AB] fait avec les tangentes au cercle en A et en B, un angle dont la mesure est égale à celle de l’angle inscrit 
.
Explications :
La droite (OB) est perpendiculaire avec la tangente en B. Donc 
.
En considérant le triangle AOB, on a 
donc 
.
Alors 
.
Remarque : Il s’agit de la proposition III.32 des Éléments d’Euclide.
