Angles

I – Notion d’angle

Définitions
  • Un angle est une portion de plan délimitée par deux demi-droites ayant la même origine.
  • L’origine des demi-droites est le sommet de l’angle.
  • Les demi-droites sont les côtés de l’angle.

Exemple :

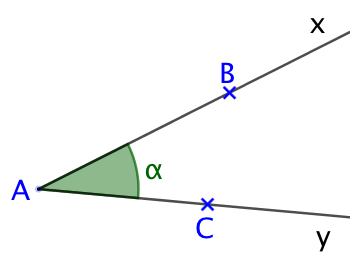
  • Le point A est le sommet de l’angle.
  • Les demi-droites [Ax) et [Ay) sont les côtés de l’angle. 

Notation : L’angle de l’exemple peut être noté : \widehat{xAy}, \widehat{yAx},\widehat{BAC},\widehat{CAB}..La lettre du milieu est toujours le sommet de l’angle.

Mesure d’un angle : Mesurer un angle consiste à mesure l’écartement de ce deux côtés. L’unité de mesure s’appelle le degré. On utilise souvent l’alphabet grec pour nommer des mesures d’angle, comme la lettre \alpha de la figure ci-dessus.

Angles de même mesure : Des angles de même mesure sont codés avec le même symbole (comme pour les longueurs).

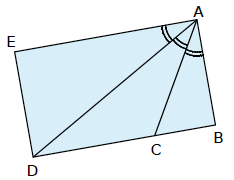
Exemple : les angles \widehat{EAD}, \widehat{DAC} et \widehat{CAB} sont de même mesure.

II – Différents types d’angles

On classe les angles par catégories selon leur mesure.

Figure Mesure Positions des côtés
Angle nul : 0° Confondus
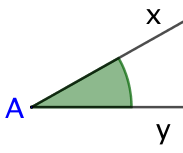Angle aigu : entre 0° et 90°
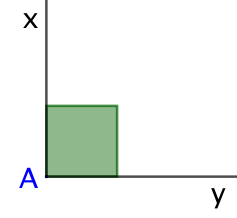Angle droit : 90° Perpendicuaires
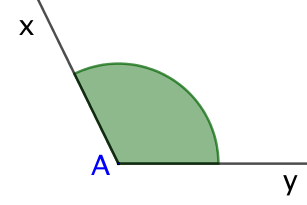Angle obtus : entre 90° et 180°
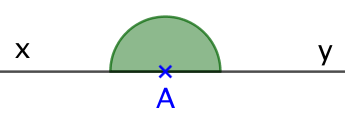Angle plat : 180° Dans le prolongement l’un de l’autre

 

Propriétés
Étant donnés trois points A, B et C,

  • Les droites (AB) et (AC) sont perpendiculaires si et seulement si l’angle 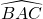\widehat{BAC} est un angle droit.
  • Les points A, B et C sont alignés si et seulement si l’angle 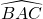\widehat{BAC} est un angle plat.

III – Utilisation du rapporteur

L’instrument qui permet de mesurer des angles est le rapporteur.

ATTENTION : Un rapporteur gradué en degrés a souvent une double graduation qui va de 0 à 180 degrés et qui est source de nombreuses erreurs. Il conviendra donc de bien observer si l’angle qu’on étudie est aigu ou obtus.

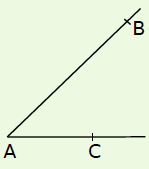
 Exemple : On va mesurer l’angle \widehat{CAB}

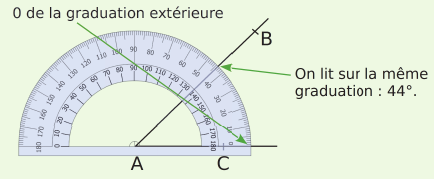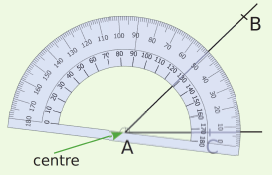
On place le centre du rapporteur sur le sommet de l’angle. On place un zéro du rapporteur sur le côté [AC). La mesure de l’angle est donnée par l’autre côté de l’angle sur la même échelle de graduation.

 

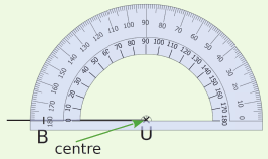
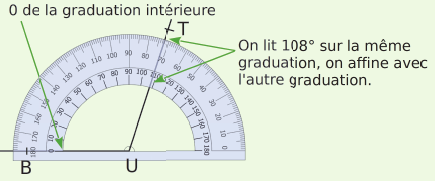
Exemple : On va construire l’angle \widehat{BUT} de mesurant 108°.

On trace d’abord une demi-droite [UB). On place le centre du rapporteur sur le point U. On place un zéro du rapporteur sur le côté [UB). On marque, d’un petit repère, 108°. On trace la demi-droite d’origine U passant par le repère. On place un point T sur cette demi-droite.

IV – Bissectrice d’un angle

Définition
La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles de même mesure.

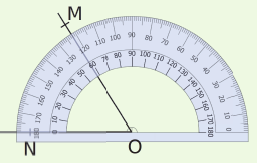
Exemple : On veut construire la bissectrice de l’angle \widehat{MON} avec un rapporteur.

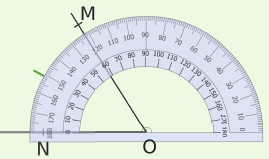
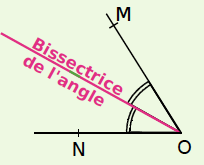
Pour construire la bissectrice de l’angle \widehat{MON}, on commence par le mesurer à l’aide du rapporteur. Il mesure 58°. On prend la moitié de cette mesure, ce qui donne 29°, et on trace un repère. On trace la demi-droite d’origine O passant par ce repère. Cette demi-droite est la bissectrice de l’angle \widehat{MON}
Print Friendly, PDF & Email