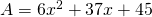Calcul littéral

I. INITIATION AU CALCUL LITTÉRAL

1) Écriture d’une expression littérale

Définition :

Une expression littérale est une expression comportant des lettres appelées variables, qui représentent des nombres.

Convention : Le signe $\times$ de la multiplication peut être supprimé devant une lettre ou devant une parenthèse.

Exemple : Le prix de $n$ stylos à $2,7$ € l’unité s’exprime en fonction de la variable $n$ par l’expression littérale : $p = 2,7 \times n = 2,7n$

2) Calcul d’une expression littérale

On peut calculer une expression littérale si on connaît la valeur de chaque variable rencontrée dans l’expression.

Exemple : L’aire d’un rectangle de longueur $L$ et de largeur $l$ est donnée par la formule $A = L \times l$ . Si on sait que $L = 7$ cm et que $l = 2$ cm, alors on peut calculer l’aire du rectangle : $A = 7 \times 2 = 14$ cm².

II. DÉVELOPPER, FACTORISER, RÉDUIRE

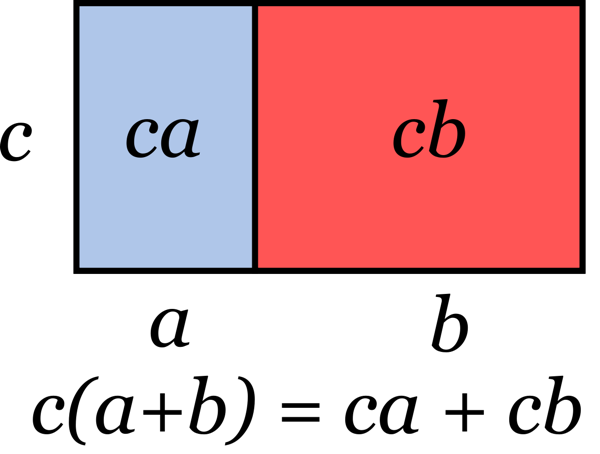
1. Développer avec la simple distributivité

$\bigstar$ Propriété : Quels que soient les nombres $a, b, k$ , on a les égalités suivantes :

On dit que la multiplication est distributive par rapport à l’addition et à la soustraction.

Définition :

Développer une expression produit, c’est la transformer en une somme ou une différence.

Exemples :

Développer l’expression $4(x+3)$ : $4(x+3) = 4 \times x + 4 \times 3 = 4x + 12$
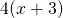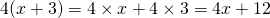
Développer l’expression $2(x-5)$ : $2(x-5) = 2 \times x - 2 \times 5 = 2x - 10$

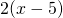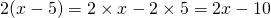
2. Factoriser une somme ou une différence

Définition :

Factoriser une expression somme ou différence, c’est la transformer en un produit de plusieurs termes appelés facteurs.

$\bigstar$ Propriété : Quels que soient les nombres $a, b, k$ , on a les égalités suivantes :

Exemples : Factoriser chacune des expressions A, B et C

$A = 7x - 14 = 7 \times x - 7 \times 2 = 7(x-2) \qquad \text{Le facteur commun est 7}$ .
$B = 6x^2 + 5x = x \times 6x + x \times 5 = x(6x+5) \qquad \text{Le facteur commun est x}$ .
$C = 6x - 3x^2 = 3x \times 2 - 3x \times x = 3x(2-x) \qquad \text{Le facteur commun est 3x}$ .

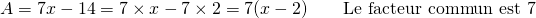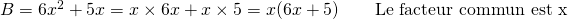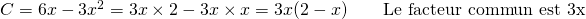3) Réduire une expression sans parenthèses

Définition :

Réduire une expression, c’est l’écrire plus simplement en diminuant le nombre de termes.

Remarque : La factorisation permet de réduire certaines expressions.

Exemples :

$5x + 7x = (5 + 7)x = 12x$
$9y - 3y = (9 - 3)y = 6y$
$3a - 8 - 10a + 2 = 3a - 10a - 8 + 2 = (3 - 10)a - 6 = -7a - 6$

4) Réduire une expression avec parenthèses

$\bigstar$ Propriété : Pour réduire une expression avec parenthèses, on doit d’abord supprimer les parenthèses avant de changer les termes de place.

Si un signe « plus » précède les parenthèses, alors on supprime le signe « plus » et les parenthèses, et on écrit tels quels les termes qui étaient entre parenthèses.
Si un signe « moins » précède les parenthèses, alors on supprime le signe « moins » et les parenthèses, et on écrit l’opposé de chaque terme situé entre parenthèses.

Exemple : réduire l’expression $A = 2(3x+8)-(4x-5) = 2 \times 3x + 2 \times 8 - 4 \times x + 5 = 6x - 4x + 16 + 5 = 2x + 21$

5) Double distributivité :

$\bigstar$ Propriété : Quels que soient les nombres $a, b, c, d$ , on a l’égalité suivante :

Exemple : Développer et réduire $A = (3x + 5)(2x + 9)$

on utilise la propriété de la double distributivité : $A = 3x \times 2x + 3x \times 9 + 5 \times 2x + 5 \times 9$
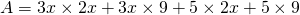
On effectue chacun des quatre produits : $A = 6x^2 + 27x + 10x + 45$
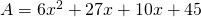
On réduit : $A = 6x^2 + 37x + 45$