Cercle construit à partir d’un segment et d’un angle

Étant donné un angle \alpha et un segment [AB], on veut construire un cercle et un angle inscrit égal à \alpha.

Construction avec \alpha < \dfrac{\pi}{2} :

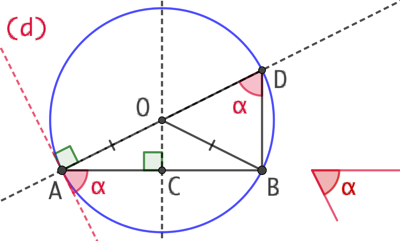
  • On place le milieu C du segment [AB].
  • On construit la médiatrice du segment [AB].
  • À partir du segment [AB], on construit un angle \alpha.
  • On construit la perpendiculaire au côté de l’angle \alpha qui n’est pas [AB] et passant par A.
  • Soit O le point d’intersection des deux perpendiculaires. O étant sur la médiatrice de [AB], OA=OB.
  • On trace le cercle de centre O passant par A et B. Il coupe la droite (AO) en D.
  • L’angle \widehat{ADB}=\alpha.

Explications :

On sait que l’angle inscrit dans un cercle et qui intercepte une corde a la même mesure que l’angle entre cette corde et les tangentes du cercle aux deux extrémités de la corde. Voir Cercle construit à partir d’un segment et d’un angle.

Remarque si \alpha = \dfrac{\pi}{2} : il suffit de construire un cercle de diamètre AB et de choisir un point D sur le cercle. Alors le triangle ABD sera rectangle en D.

Remarque : Il s’agit de la proposition III.33 des Éléments d’Euclide.

Print Friendly, PDF & Email