À partir d’un triangle quelconque, on construit 6 points particuliers qui appartiennent tous au même cercle, dit de Conway.
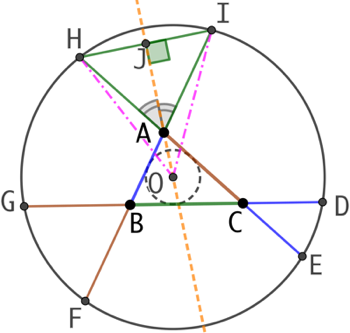Construction : soit ABC un triangle quelconque et soit O le centre du cercle inscrit à ABC.
- D est le point de la demi-droite [BC) tel que CD = AB ;
- E est le point de la demi-droite [AC) tel que CE = AB ;
- F est le point de la demi-droite [AB) tel que BF = AC ;
- G est le point de la demi-droite [CB) tel que BG = AC ;
- H est le point de la demi-droite [CA) tel que AH = BC ;
- I est le point de la demi-droite [BA) tel que AI = BC ;
- Les ponts D, E, F, G, H et I appartient au cercle de centre O.
Explications :
Par construction, AH = AI, donc HAI est un triangle isocèle en A. Par conséquent la médiatrice de [HI] est confondue avec la bissectrice de 
, notée (AJ).
(AJ) est aussi la bissectrice de 
. Donc le point O appartient à la droite (AJ). Puisque (AJ) est aussi la médiatrice de [HI], O est équidistant de H et de I.
De la même façon on démontre O est aussi équidistant des points I et D, puis de E, F et G. Ce qui démontre que les 6 points sont cocycliques, de centre O.
