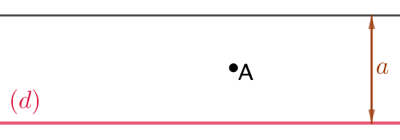
Étant donnés un point A, une droite (d) et une longueur ![]() , on veut tracer le cercle passant par A, de longueur
, on veut tracer le cercle passant par A, de longueur ![]() et tangent à (d).
et tangent à (d).
 |
 |
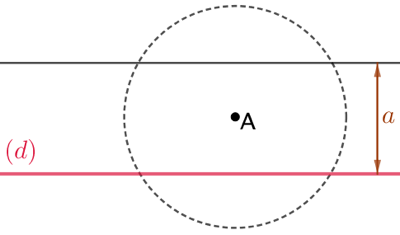 |
| Le centre du cercle doit être à une longueur |
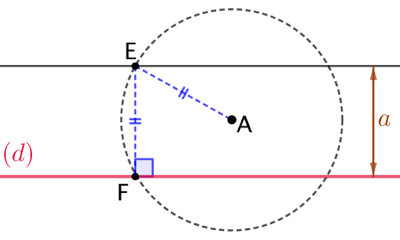
On trace une droite parallèle à (d) et distante de (d) d’une longueur |
A est sur ce cercle donc le centre du cercle doit être à une distance |
 |
 |
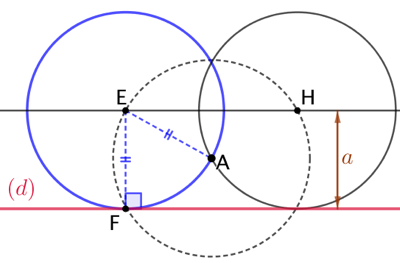 |
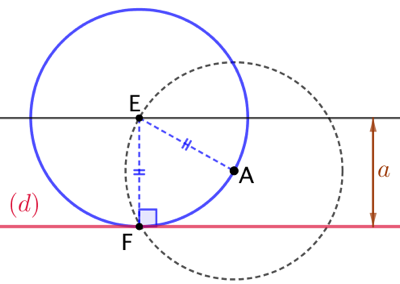
| Donc le centre du cercle recherché est le point E dont le projeté orthogonal sur (d) est F. |
On vérifie bien que ce cercle passe par A et est tangent à (d). | Il existe un second cercle de centre H. |
Condition d’existence du cercle : il faut que la distance entre le point A et la droite soit inférieure à ![]() .
.
