Cercle de rayon donné tangent à deux droites

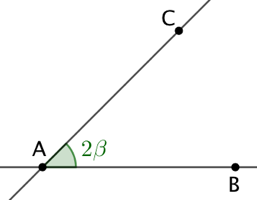
Soient deux droites sécantes (AB) et (AC) faisant entre elles un angle de mesure . On cherche à tracer un cercle de rayon qui soit tangent à ces deux droites.

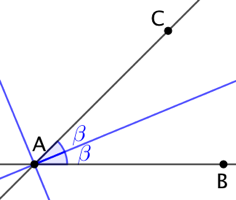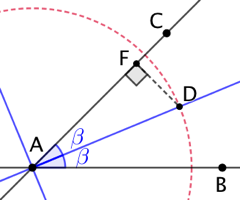Si le cercle est tangent à (AB) et à (AC) alors son centre D est à égal distance de (AB) et de (AC). Donc D est sur l’une des bissectrices de . Soit F le projeté orthogonal de D sur (AC). FD est le rayon du cercle recherché. Alors . On trace le cercle de centre A et de rayon . L’intersection de ce cercle avec la bissectrice est le point D. Le cercle recherché est donc le cercle de centre D et passant par F.
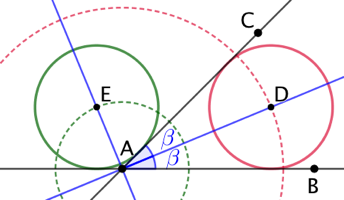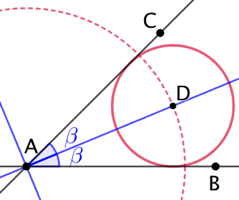
		Il existe en réalité 4 cercles répondant au problème posé, autant que de demi-bissectrices. Ci-contre un cercle dans l’angle complémentaire à .

Remarque : Si ces deux droites sont parallèles et que la distance entre elles soit de alors il existe une infinité de solutions : ce sont tous les cercles dont le centre se situe sur la droite placée entre les deux droites et à une distance de chacune d’elles.

Sinon, il n’y a aucune solution.