 Soit un triangle ABC et un angle
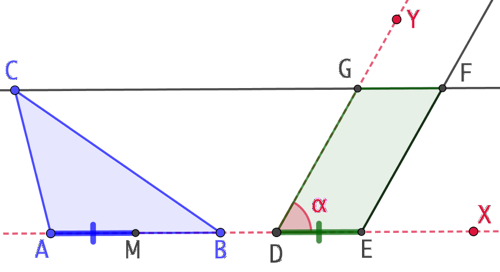
Soit un triangle ABC et un angle ![]() . On veut construire un parallélogramme DEFG dont l’un des angles est
. On veut construire un parallélogramme DEFG dont l’un des angles est ![]() et dont l’aire est égale à celle du triangle ABC.
et dont l’aire est égale à celle du triangle ABC.
Construction :
- On trace sur la droite (AB) un segment [DE] de longueur
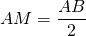 .
. - On trace la droite parallèle à (AB) et passant par G. Elle coupe (DY) en G.
- On trace la droite parallèle à (DY) et qui passe par E. Elle coupe (CG) en F.
Explications :
Par construction le quadrilatère DEFG est un parallélogramme puis que ces côtés sont portés par des droites parallèles.
Si un parallélogramme et un triangle possèdent une base de même longueur et sont construits entre deux droites parallèles, alors l’aire du parallélogramme est le double de celle du triangle. SI la base du parallélogramme est la moitié de celle du triangle alors les deux figures ont la même aire. Ce qui est le cas pour ABC et DEFG. Voir : Un parallélogramme et un triangle
Remarque : Il s’agit de la proposition I.42 des Éléments d’Euclide.
