Copie d’un angle

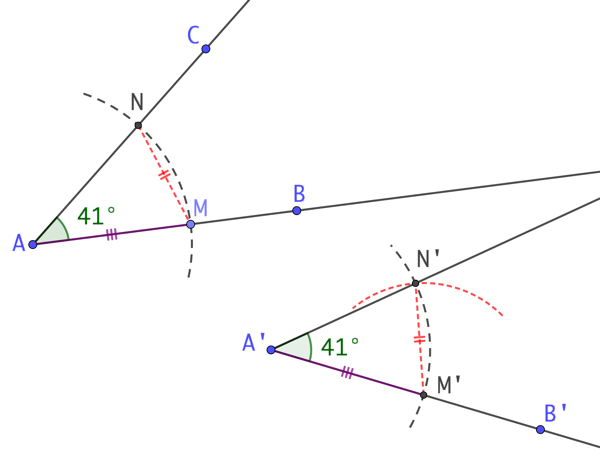
On construit la copie d’un angle $\widehat{BAC}$ ainsi :

On trace une demi-droite [A’B’).
On choisit un point quelconque M sur [AB) et on trace le cercle de centre A passant par M. Ce cercle coupe [AC) au point N.
On trace un un cercle de centre A’ et de même rayon que le premier cercle.
On trace un troisième cercle de centre M’ et de rayon la distance MN.
L’intersection du deuxième et du troisième cercle est noté N’. L’angle 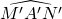$\widehat{M'A'N'}$ a la même mesure que l’angle MAN.

Explications :

Le triangle MAN est isocèle en A. AM = AN

N’ appartient au cercle de centre A’ et de rayon A’M’ donc M’A’N’ est isocèle en A’.
A’M = A’N = AM.

Par construction MN = M’N’. Donc les triangles MAN et M’A’N’ sont isométriques donc possèdent des angles de même mesure.

Remarque : Il s’agit de la proposition n°I.23 des Éléments d’Euclide.