L’objectif est de retrouver la formule donnant le sinus et le cosinus d’une somme d’angles à partir d’une construction géométrique. Pour simplifier la démonstration, on considère deux angles positifs dont la somme est inférieure à 90°.
Solution n°1
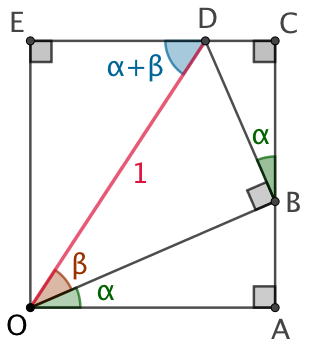 Construction :
Construction :
- un triangle OAB rectangle en A. La mesure de l’angle
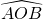 est
est 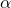 .
. - un triangle OBD rectangle en B. La mesure de l’angle
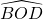 est
est 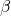 .
. - Sur la demi-droite [AB), on place le point C de telle manière que le triangle BCD soit rectangle en C.
- Sur la demi-droite [CD), on place le point E de telle manière que le triangle ODE soit rectangle en E.
De cette construction, il vient que la mesure de l’angle ![]() est
est ![]() et que celle de
et que celle de ![]() est
est ![]() .
.
Afin de simplifier les calculs, on convient de prendre la distance OD comme unité de mesure. Alors :
Dans le triangle OBD :
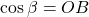
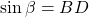 ;
;
Dans le triangle OAB :
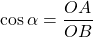 donc
donc 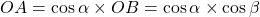 .
.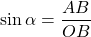 donc
donc 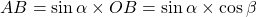 .
.
Dans le triangle BCD :
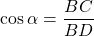 donc
donc 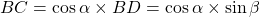
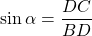 donc
donc 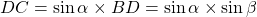
dans le triangle ODE :
Solution n°2
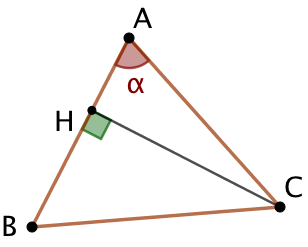 1ère étape : Aire d’un triangle connaissant la mesure d’un angle et les longueurs des deux côtés de cet angle.
1ère étape : Aire d’un triangle connaissant la mesure d’un angle et les longueurs des deux côtés de cet angle.
L’aire du triangle ABC est donnée par l’expression : ![]() .
.
![]() donc
donc ![]() .
.
L’aire du triangle devient : ![]() .
.
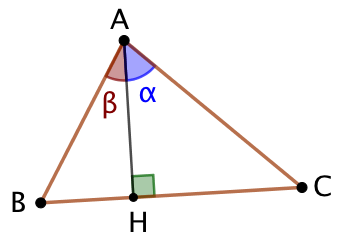 2ème étape :
2ème étape : ![]()
On écrit que l’aire du triangle ABC est la sommes des aires des triangles ABH et ACH : ![]() . (1)
. (1)
Dans le triangle ABH : ![]() et dans le triangle ACH :
et dans le triangle ACH : ![]() .
.
L’égalité (1) devient : ![]() .
.
Après simplification par ![]() , on obtient :
, on obtient : ![]()
Voir : Somme de sinus et de cosinus
