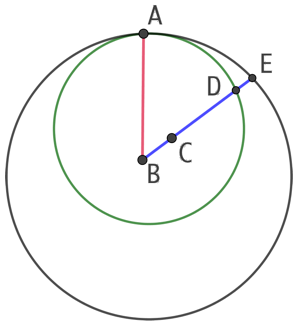
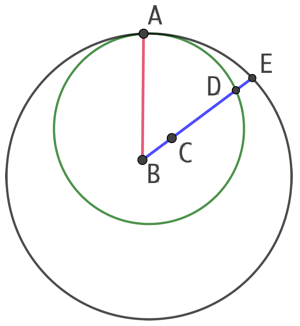
Deux cercles de centre B et C sont tangents en un point A. L’un des cercles se trouve à l’intérieur de l’autre. Alors les points A, B et C sont alignés.
Explications :
Raisonnons par l’absurde en supposant que A, B et C ne sont pas alignés. La droite (BC) coupe les deux cercles en D et E.
On peut écrire alors que : BA = BE puisque A et E appartiennent au cercle de centre B.
Considérons le cercle de centre C. [CD] est un rayon de ce cercle et B, C, D sont alignés. Donc d’après la proposition III.7 d’Euclide, BA < BD.
Mais si BA = BE, cela implique que BE < BD, ce qui est impossible.
Remarque : Il s’agit de la proposition III.11 des Éléments d’Euclide.
