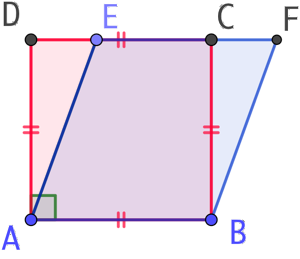
Deux parallélogrammes, ABCD et ABFE, construits sur des bases de même longueur AB et entre les mêmes parallèles (AB) et (DF), ont la même aire :
Explications :
Le parallélogramme ABCD est un carré. On sait que son aire vaut AB2.
Le parallélogramme ABFE a comme base [AB] et comme hauteur [AD]. Donc son aire est AB x AD. Mais ABCD est un carré donc AD = AB. Par conséquent l’aire de ABFE vaut aussi AB2.
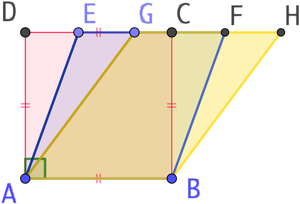Dans la seconde figure on a ajouté un parallélogramme ABHG (jaune) qui a la même base que le carré ABCD et qui est construit entre les mêmes parallèles. Ces deux parallélogrammes ont la même aire d’après les explications précédentes. Par conséquent les parallélogrammes ABFE et ABHG ont la même aire.
Remarque : le raisonnement serait le même si ABCD était un rectangle et non un carré, mais possédant un côté de même longueur que la base du parallélogramme et un autre côté de longueur égale à la hauteur du parallélogramme.
Remarque : Euclide s’appuie sur la notion de triangles isométriques, d’ajouts et de soustractions d’aires de triangles.
Remarque : Il s’agit des propositions I.35 et I.36 des Éléments d’Euclide.
