 Étant donnés un segment et un point, comment construire un second segment à partir de ce point et ayant une longueur égale à celle du premier segment ?
Étant donnés un segment et un point, comment construire un second segment à partir de ce point et ayant une longueur égale à celle du premier segment ?
Construction :
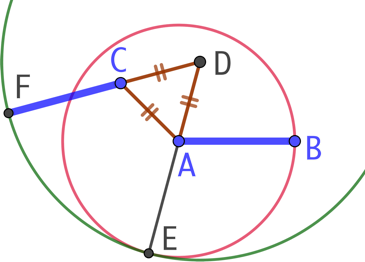
On souhaite dupliquer le segment [AB] en un segment dont l’une des extrémités est le point C.
- On trace le triangle équilatéral ADC.
- On trace le cercle de centre A et de rayon AB.
- La droite (DA) coupe ce cercle au point E.
- On trace le cercle de centre D et de rayon DE.
- La droite (DC) coupe ce second cercle au point F. Le segment [CF] a la même longueur que [AB].
Explications :
(1) ![]() et
et ![]() .
.
Par construction les points E et F appartiennent au cercle de centre D et de rayon DE, donc ![]() .
.
De plus ADC est un triangle équilatéral donc ![]() .
.
De l’égalité (1) il vient donc que ![]() .
.
Comme E et B appartiennent au cercle de centre A et de rayon AB, on a donc ![]() . Mais comme
. Mais comme ![]() , on peut conclure que
, on peut conclure que ![]() .
.
Remarque : Il s’agit de la proposition I.2 des Éléments d’Euclide.
