 Étant donné un segment [AB] et un nombre réel
Étant donné un segment [AB] et un nombre réel ![]() positif et différent de 1, il existe deux point C et G tels que
positif et différent de 1, il existe deux point C et G tels que ![]() .
.
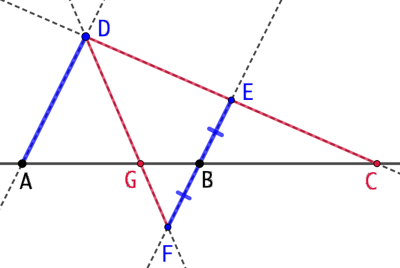
Construction :
- On trace une droite passant par A;
- On place sur cette droite un point D.
- On trace une droite parallèle à (AD) passant par B
- On place sur cette droite un point E tel que
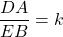 .
. - La droite (ED) coupe la droite (AB) au point C.
- On place le point F symétrique du point E par rapport à B.
- La droite (DF) coupe la droite (AB) en G.
Explications :
(AD) et (BE) sont parallèles.
On utilise le théorème de Thalès dans ADC : ![]() . Ainsi C est l’un des deux points recherchés.
. Ainsi C est l’un des deux points recherchés.
On utilise le théorème de Thalès dans ADFB : ![]() . G est l’autre point recherché.
. G est l’autre point recherché.
Remarque : Pour plus de rigueur il conviendrait de raisonner en mesure algébrique.
Moyenne harmonique : AB est la moyenne harmonique de AG et de AC, c’est-à-dire que ![]() .
.
![]() donc
donc ![]() . D’où
. D’où ![]()
![]() .
.
Cas extrême : ![]() , alors G est le milieu de [AB], donc
, alors G est le milieu de [AB], donc ![]() .
.
L’égalité ![]() devient
devient ![]() , ce qui implique que
, ce qui implique que ![]() , autrement dit que la distance AC tend vers l’infini.
, autrement dit que la distance AC tend vers l’infini.
Voir également : Bissectrices et division harmonique
