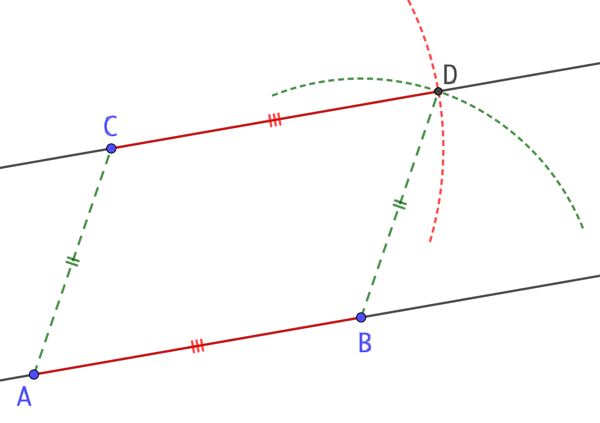
On construit la droite parallèle à la droite (AB) passant par le point C ainsi :
- On trace le cerce de centre C et de rayon la longueur AB.
- On trace le cercle de centre B et de rayon la distance AC.
- Les deux cercles se coupent en un point D. La droite (CD) est parallèle à (AB).
Explications :
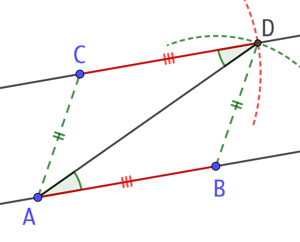
Première version : Par construction, le quadrilatère ABDC a ses côtés opposés de même longueur. C’est donc un parallélogramme. Par définition du parallélogramme, on peut alors affirmer que (CD) et (AB) sont parallèles.
Deuxième version : Par construction, les triangles ABD et ACD sont isométriques, c’est-à-dire que leurs trois côtés sont deux de même longueur. Donc les deux triangles ont leurs angles opposés de même mesure. En particulier les angles BAD et ADC qui sont alternes-internes ont la même mesure. On en déduit que les droites (AB) et (CD) sont parallèles.
Remarque :
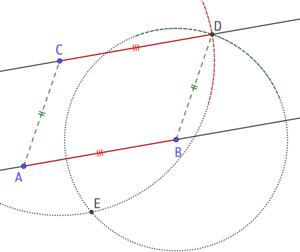
En réalité les deux cercles se coupent en un second point E. Evidemment on ne retient pas ce point car la droite (CE) n’est visiblement pas parallèle à (AB). Le point D convient car il est situé du même côté que C par rapport à (AB).
On note que ce protocole permet de construire un parallélogramme.
Remarque : Il s’agit de la proposition I.31 des Éléments d’Euclide.
