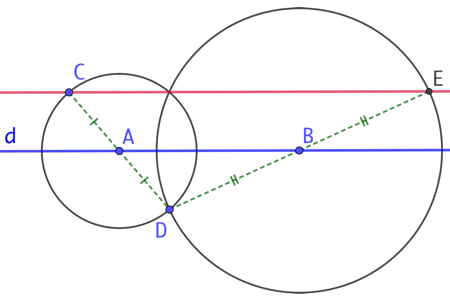
On construit la droite parallèle à la droite d passant par le point C ainsi :
- On place deux points A et B sur d pas trop éloignés de C.
- On trace le cercle de centre A et passant par C. Ce cercle coupe la droite (AC) en D.
- On trace le cercle de centre B passant D. Ce cercle coupe la droite (BD) en E. (CE) est la droite recherchée.
Explications :
Par construction D est le symétrique de C par rapport A et E est le symétrique de D par rapport à B. Donc A est le milieu de [CD] et B est le milieu de [DE]. On applique le théorème des milieux au triangle CDE et on peut alors affirmer que les droites (AB) et (CE) sont parallèles.
Remarque : deux autres constructions d’une parallèle d’une droite :
