I – Droites sécantes et angles
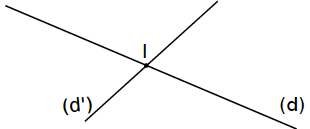 Exemple : Le point I est le point d’intersection des droites (d) et (d’).
Exemple : Le point I est le point d’intersection des droites (d) et (d’).
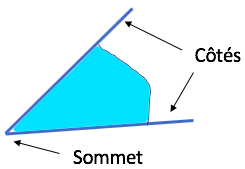 Un angle est une portion de plan délimitée par deux demi-droites ayant la même origine.
Un angle est une portion de plan délimitée par deux demi-droites ayant la même origine.- Les deux demi-droites s’appellent les côtés de l’angle.
- L’origine commune des deux demi-droites s’appelle le sommet de l’angle.
- La mesure d’un angle est l’écartement de ses deux côtés.
II – Longueur d’un segment
III – Droites parallèles
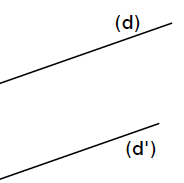 Exemple : Les droites (d) et (d’) sont parallèles. Elles ne se coupent pas. Elles n’ont pas de point d’intersection.
Exemple : Les droites (d) et (d’) sont parallèles. Elles ne se coupent pas. Elles n’ont pas de point d’intersection.
On note : (d) // (d’)
Construction d’une droite parallèle à une autre droite
| On va tracer la droite parallèle à la droite |
 |
| On choisit deux points quelconques On trace un arc de cercle de centre |
 |
| On trace un arc de cercle de centre |
 |
| Soit La droite |
 |
 Exemple :
Exemple :
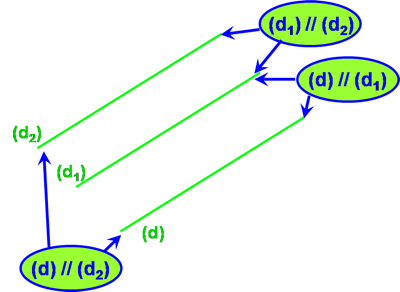
- On sait que (d2) est parallèle à (d1) et que (d) est aussi parallèle à (d1).
- On en déduit donc que (d) est parallèle à (d2).
IV – Droites perpendiculaires
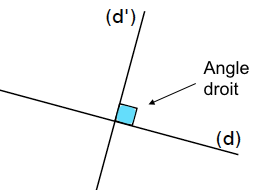 Exemple :
Exemple :
La droite (d’) est perpendiculaire à la droite (d).
On peut aussi dire que la droite (d) est perpendiculaire à la droite (d’).
Remarque : Deux droites perpendiculaires forment entre elle quatre angles droits.
Notation : (d) est perpendiculaire à la droite (d’) se note : ![]() .
.
Codage : Pour indiquer que deux droites sont perpendiculaires ou qu’un angle est droit, on code la figure avec un petit carré (ici le carré bleu).
Construction de la perpendiculaire à une droite
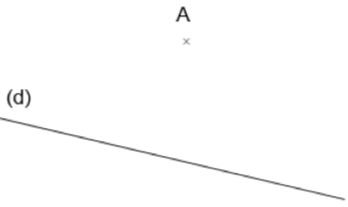
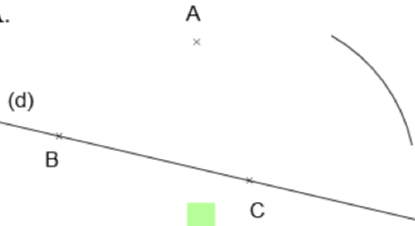
| On va tracer la droite perpendiculaire à (d) qui passe par le point A. | 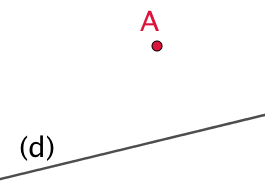 |
| On choisit deux points quelconques B et C sur la droite (d). | 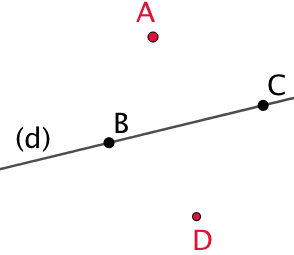 |
| On trace un arc de cercle de centre B passant par A.
|
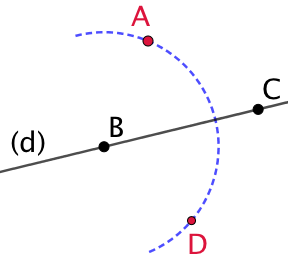 |
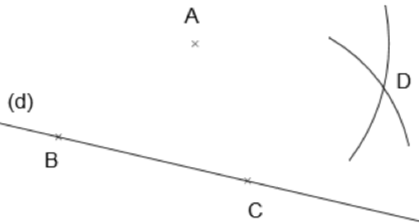
| On trace un arc de cercle de centre C passant par A. | 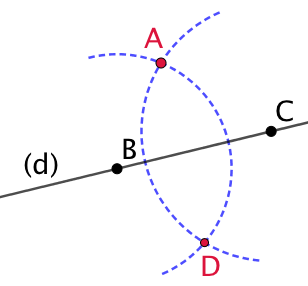 |
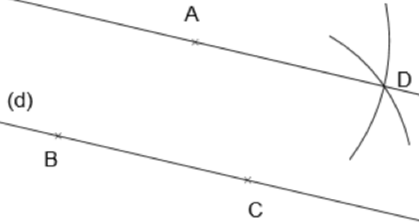
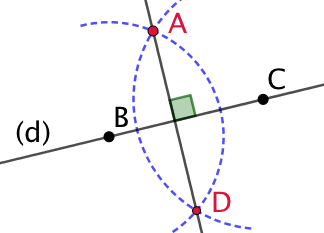
| Ces arcs de cercle se croisent au point D. La droite (AD) est la droite perpendiculaire à (d) et passant par A.
On code la figure pour indiquer que les deux droites sont perpendiculaires. |
 |
 Exemple :
Exemple :
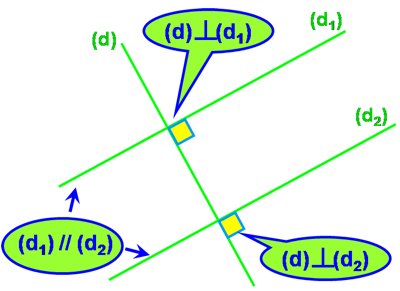
- On sait que (d1) est perpendiculaire à (d) et que (d2) est aussi perpendiculaire à (d).
- Alors (d1) et (d2) sont parallèles.
Exemple : On utilise à nouveau la figure précédente.
- On sait que (d1) et (d2) sont parallèles et que (d) est perpendiculaire à (d1).
- Alors (d) est aussi perpendiculaire à (d2).
V – Distance d’un point à une droite
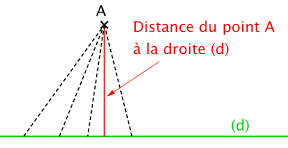 Soient une droite
Soient une droite ![]() et un point A. On construit plusieurs segments ayant comme extrémités
et un point A. On construit plusieurs segments ayant comme extrémités ![]() et des points de la droite
et des points de la droite ![]() .
.
On observe qu’il existe un point particulier de la droite ![]() pour lequel le segment le reliant au point
pour lequel le segment le reliant au point ![]() a une longueur minimale.
a une longueur minimale.
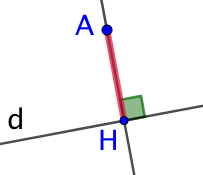 Soient une droite
Soient une droite La distance entre ![]() et
et ![]() est la longueur du segment
est la longueur du segment ![]() .
.
![]() est le segment le plus court reliant
est le segment le plus court reliant ![]() et tous les points de la droite
et tous les points de la droite ![]() .
.
EXERCICES
- 1 / 117 : écriture
- 3, 4 / 117 : construction
- 10 / 118 : vocabulaire
- 11 / 118 : recherche
- 12 / 118 : Raisonnement
- 19, 21 / 119 : programme de construction
- 23, 24, 25 / 120 : constructions
- 36 / 121 : construction et symboles
- 59 / 126 : Programme de construction complexe
- 63 / 127 : belle figure géométrique à reproduire
