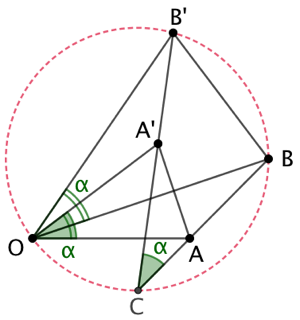
Soit une rotation de centre O et d’angle 
. Soient deux points A et B et leurs images A’ et B’ par la rotation. Alors les droites (AB) et (A’B’) font entre elles un angle de mesure .
Explications :
Les triangles OAB et OA’B’ sont isométriques puisqu’une rotation conserve les polygones.
Donc 
, soit 
.
Par conséquent les points O,C, B et B’ sont cocycliques. Alors 
puisque ces angles interceptent la corde [BB’]. Ainsi 
mesure .
