Dans ce chapitre, on se place dans un plan, un repère orthonormé ![]() et une base orthonormée
et une base orthonormée ![]() .
.
I – Vecteur directeur d’une droite
 Exemple :
Exemple :
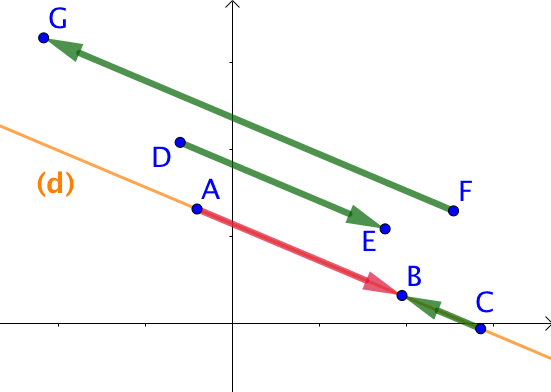
Sur la figure de droite, tous les vecteurs de couleur verte sont colinéaires au vecteur ![]() . Ce sont tous des vecteurs directeurs de la droite (d).
. Ce sont tous des vecteurs directeurs de la droite (d).
Bien évidemment, ![]() est aussi un vecteur directeur de (d).
est aussi un vecteur directeur de (d).
Conséquences :
- Une droite a une infinité de vecteurs directeurs.
- Tous les vecteurs directeurs d’une droite sont colinéaires entre eux.
Démonstration : Si ![]() est un vecteur directeur de la droite passant par
est un vecteur directeur de la droite passant par ![]() , alors il existe un point
, alors il existe un point ![]() tel que
tel que ![]() et
et ![]() sont colinéaires.
sont colinéaires.
Soit ![]() un point quelconque de cette droite, alors les points
un point quelconque de cette droite, alors les points ![]() ,
, ![]() et
et ![]() sont alignés, ce qui implique que les vecteurs
sont alignés, ce qui implique que les vecteurs ![]() et
et ![]() sont colinéaires.
sont colinéaires.
Sachant que ![]() et
et ![]() sont colinéaires, il vient que
sont colinéaires, il vient que ![]() et
et ![]() sont colinéaires.
sont colinéaires.
II – Équation cartésienne d’une droite
À partir d’un exemple
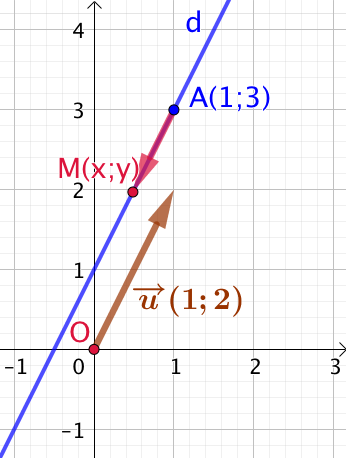 Considérons la droite
Considérons la droite ![]() passant par
passant par ![]() et de vecteur directeur
et de vecteur directeur ![]() .
.
Soit ![]() un point quelconque de la droite
un point quelconque de la droite ![]() . Les coordonnées du vecteur
. Les coordonnées du vecteur ![]() sont
sont ![]() et
et ![]() .
.
Alors nous savons que les vecteurs ![]() et
et ![]() sont colinéaires. Donc leur déterminant est nul :
sont colinéaires. Donc leur déterminant est nul : ![]() .
.
On développe cette égalité : ![]() .
.
On la simplifie : ![]() . Cette relation est l’équation cartésienne de la droite
. Cette relation est l’équation cartésienne de la droite ![]() . Cette équation est la « carte d’identité » de la droite. Tout ce que l’on peu savoir sur cette droite est contenu dans cette relation. Plus précisément elle définit qu’un point appartient à cette droite à la condition que ses coordonnées
. Cette équation est la « carte d’identité » de la droite. Tout ce que l’on peu savoir sur cette droite est contenu dans cette relation. Plus précisément elle définit qu’un point appartient à cette droite à la condition que ses coordonnées ![]() soit une solution de l’équation.
soit une solution de l’équation.
Vérifions à l’aide de cette équation que le point ![]() appartient bien à
appartient bien à ![]() . Pour cela remplaçons dans l’équation
. Pour cela remplaçons dans l’équation ![]() ,
, ![]() par
par ![]() :
:
![]() est bien égal à 0 dont
est bien égal à 0 dont ![]() est bien une solution de l’équation
est bien une solution de l’équation ![]() . Cela suffit pour vérifier que
. Cela suffit pour vérifier que ![]() est sur la droite
est sur la droite ![]() .
.
Question : Puisque cette équation est la carte d’identité de la droite, on devrait la retrouver en prenant un autre point de la droite, choisi à la place de ![]() et en prenant un autre vecteur directeur de cette droite, choisi à la place de
et en prenant un autre vecteur directeur de cette droite, choisi à la place de ![]() .
.
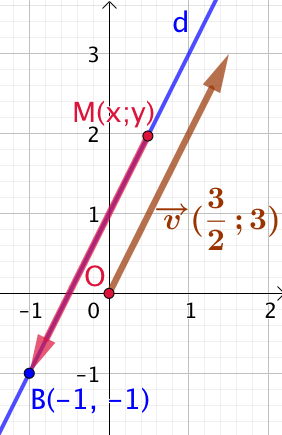 Soient le point
Soient le point ![]() de la droite
de la droite ![]() et
et ![]() , un autre vecteur directeur de
, un autre vecteur directeur de ![]() . Je laisse à l’élève le soin de vérifier que
. Je laisse à l’élève le soin de vérifier que ![]() et
et ![]() sont bien colinéaires.
sont bien colinéaires.
On va reprendre à l’identique ce qui a été fait avec ![]() et
et ![]() .
.
Soit ![]() un point quelconque de la droite
un point quelconque de la droite ![]() . Les coordonnées du vecteur
. Les coordonnées du vecteur ![]() sont
sont ![]() et
et ![]() .
.
![]() et
et ![]() sont colinéaires. Donc leur déterminant est nul :
sont colinéaires. Donc leur déterminant est nul : ![]() .
.
On développe cette égalité : ![]() .
.
On la simplifie : ![]() .
.
On multiple chaque membre de l’égalité par ![]() :
: ![]()
On divise chaque membre de légalité par ![]() :
: ![]() , c’est-à-dire :
, c’est-à-dire : ![]() . C’est bien l’équation cartésienne de la droite
. C’est bien l’équation cartésienne de la droite ![]() . Elle ne dépend pas du point et du vecteur directeur choisis.
. Elle ne dépend pas du point et du vecteur directeur choisis.
L’équation cartésienne d’une droite est de la forme : ![]() pour laquelle
pour laquelle ![]() ,
, ![]() et
et ![]() sont des nombres réels fixes.
sont des nombres réels fixes.
Démonstration : Soit la droite ![]() passant par
passant par ![]() et de vecteur directeur
et de vecteur directeur ![]() .
.
Soit ![]() un point quelconque de la droite
un point quelconque de la droite ![]() . Les coordonnées du vecteur
. Les coordonnées du vecteur ![]() sont
sont ![]() et
et ![]() .
.
Alors nous savons que les vecteurs ![]() et
et ![]() sont colinéaires. Donc leur déterminant est nul :
sont colinéaires. Donc leur déterminant est nul : ![]() .
.
On développe cette égalité : ![]() que l’on présente ainsi :
que l’on présente ainsi : ![]() . C’est l’équation cartésienne de la droite
. C’est l’équation cartésienne de la droite ![]() .
.
En posant : ![]() ,
, ![]() et
et ![]() , on retrouve bien une équation de la forme
, on retrouve bien une équation de la forme ![]() .
.
 REMARQUE : L’équation cartésienne d’une droite n’est pas une unique. Si
REMARQUE : L’équation cartésienne d’une droite n’est pas une unique. Si ![]() est une équation cartésienne d’une droite alors pour tout réel
est une équation cartésienne d’une droite alors pour tout réel ![]() non nul, l’équation :
non nul, l’équation : ![]() est aussi une équation cartésienne de la même droite.
est aussi une équation cartésienne de la même droite.
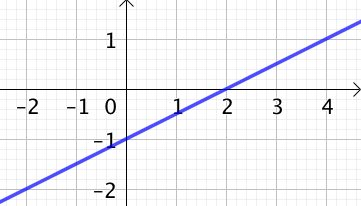
La droite représentée ci-contre a comme équation cartésienne : ![]() . En multipliant par
. En multipliant par ![]() les deux termes de cette équation, on obtient une autre équation cartésienne de cette droite :
les deux termes de cette équation, on obtient une autre équation cartésienne de cette droite : ![]() .
.
- Si
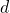 est une droite parallèle à l’axe des ordonnées, alors il existe un nombre réel
est une droite parallèle à l’axe des ordonnées, alors il existe un nombre réel 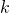 tel qu’une équation cartésienne de
tel qu’une équation cartésienne de 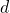 est
est 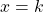 .
. - Si
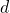 est une droite parallèle à l’axe des abscisses, alors il existe un nombre réel
est une droite parallèle à l’axe des abscisses, alors il existe un nombre réel 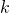 tel qu’une équation cartésienne de
tel qu’une équation cartésienne de 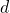 est
est 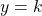 .
.
Démonstration :
Si ![]() est parallèle à l’axe des ordonnées, le vecteur
est parallèle à l’axe des ordonnées, le vecteur ![]() est un vecteur directeur de
est un vecteur directeur de ![]() .
.
Soit ![]() un point particulier de
un point particulier de ![]() . On a vu dans la démonstration précédente que si
. On a vu dans la démonstration précédente que si ![]() est un point de
est un point de ![]() alors le déterminant des vecteurs
alors le déterminant des vecteurs ![]() et
et ![]() est nul.
est nul.
Cela conduit à l’égalité : ![]() , soit
, soit ![]() ou plus simplement
ou plus simplement ![]() .
.
En posant ![]() , on obtient une équation cartésienne de
, on obtient une équation cartésienne de ![]() :
: ![]() .
.
La démonstration concernant les droites parallèles à l’axe des abscisses est très proche.
Démonstration :
 1er cas :
1er cas : ![]() . Alors l’équation
. Alors l’équation ![]() se réduit à
se réduit à ![]() , soit
, soit ![]() et finalement
et finalement ![]() .
.
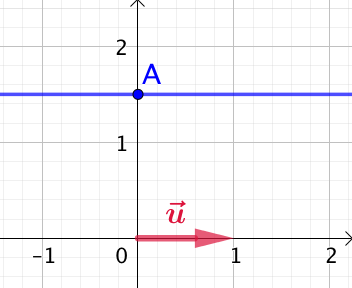
Ainsi tous les points de ![]() ont la même pour ordonnée :
ont la même pour ordonnée : ![]() , quelle que soit la valeur de leurs abscisses. Conclusion :
, quelle que soit la valeur de leurs abscisses. Conclusion : ![]() est la droite parallèle à l’axe des abscisses passant, par exemple, par le point
est la droite parallèle à l’axe des abscisses passant, par exemple, par le point ![]() de coordonnées
de coordonnées ![]() .
.
Un vecteur directeur de ![]() est
est ![]() .
.
Dans l’exemple de droite : ![]() et
et ![]() .
.
 2ème cas :
2ème cas : ![]() . Alors l’équation
. Alors l’équation ![]() se réduit à
se réduit à ![]() , soit
, soit ![]() et finalement
et finalement ![]() .
.
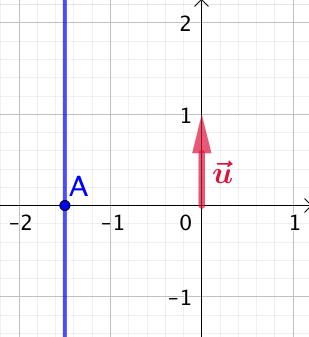
Ainsi tous les points de ![]() ont la même pour abscisse :
ont la même pour abscisse : ![]() , quelle que soit la valeur de leurs ordonnées. Conclusion :
, quelle que soit la valeur de leurs ordonnées. Conclusion : ![]() est la droite parallèle à l’axe des ordonnées passant, par exemple, par le point
est la droite parallèle à l’axe des ordonnées passant, par exemple, par le point ![]() de coordonnées
de coordonnées ![]() .
.
Un vecteur directeur de ![]() est
est ![]() .
.
Dans l’exemple de droite : ![]() et
et ![]() .
.
3ème cas : ![]() ,
, ![]() et
et ![]() . Alors l’équation
. Alors l’équation ![]() se réduit à
se réduit à ![]() . On peut découvrir deux points de
. On peut découvrir deux points de ![]() :
: ![]() et
et ![]() . Les coordonnées de
. Les coordonnées de ![]() sont évidemment
sont évidemment ![]() .
.
Soit ![]() un point quelconque de
un point quelconque de ![]() . Les coordonnées de
. Les coordonnées de ![]() sont
sont ![]() .
.
Le déterminant de ![]() et
et ![]() est
est ![]() .
.
 Or
Or ![]() donc
donc ![]() . Par conséquent le déterminant de
. Par conséquent le déterminant de ![]() et
et ![]() est nul, donc les deux vecteurs sont colinéaires, c’est-à-dire que les trois points
est nul, donc les deux vecteurs sont colinéaires, c’est-à-dire que les trois points ![]() ,
, ![]() et
et ![]() sont alignés :
sont alignés : ![]() est un point de la droite
est un point de la droite ![]() .
.
Avant de conclure que ![]() est la droite
est la droite ![]() , il faut démontrer, qu’inversement, tout point de
, il faut démontrer, qu’inversement, tout point de ![]() appartient à
appartient à ![]() :
:
Soit ![]() . Alors
. Alors ![]() et
et ![]() sont colinéaires, donc leur déterminant est nul, ce qui donne l’égalité :
sont colinéaires, donc leur déterminant est nul, ce qui donne l’égalité : ![]() , soit
, soit ![]() . Donc
. Donc ![]() .
.
On peut donc en conclure que ![]() est la droite
est la droite ![]() .
.
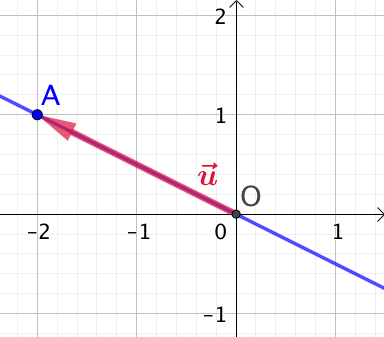
Dans l’exemple ci-contre : ![]() et
et ![]() .
.
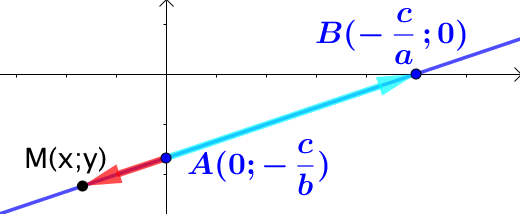 4ème cas :
4ème cas : ![]() ,
, ![]() et
et ![]() . Les deux points
. Les deux points ![]() et
et ![]() obtenus précédemment appartiennent à
obtenus précédemment appartiennent à ![]() et ne sont pas confondus puisque
et ne sont pas confondus puisque ![]() . Donc
. Donc ![]() .
.
Les coordonnées du vecteur ![]() sont
sont ![]() .
.
Soit ![]() un point quelconque de
un point quelconque de ![]() . Les coordonnées du vecteur
. Les coordonnées du vecteur ![]() sont
sont ![]() .
.
Calculons le déterminant des vecteurs ![]() et
et ![]() :
:
![]()
Or par hypothèse ![]() donc les coordonnées de
donc les coordonnées de ![]() vérifient l’équation
vérifient l’équation ![]() . Par conséquent le déterminant des vecteurs
. Par conséquent le déterminant des vecteurs ![]() et
et ![]() est nul.
est nul.
Cela signifie que ces deux vecteurs sont colinéaires, donc les points ![]() ,
, ![]() et
et ![]() sont alignés. Conclusion : tout point de
sont alignés. Conclusion : tout point de ![]() appartient à la droite
appartient à la droite ![]() .
.
Avant de conclure que ![]() est la droite
est la droite ![]() , il faut démontrer, qu’inversement, tout point de
, il faut démontrer, qu’inversement, tout point de ![]() appartient à
appartient à ![]() :
:
Soit ![]() . Alors
. Alors ![]() et
et ![]() sont colinéaires, donc leur déterminant est nul, ce qui donne l’égalité :
sont colinéaires, donc leur déterminant est nul, ce qui donne l’égalité : ![]() .
.
Alors ![]() . Comme
. Comme ![]() , il vient
, il vient ![]() . Donc
. Donc ![]() .
.
On peut donc en conclure que ![]() est la droite
est la droite ![]() .
.
Dernier point à vérifier : le vecteur ![]() est-il un vecteur directeur de
est-il un vecteur directeur de ![]() ? Comme
? Comme ![]() , il est évident que
, il est évident que ![]() est un vecteur directeur de
est un vecteur directeur de ![]() .
.
Posons ![]() . Notons que
. Notons que ![]() . Le vecteur
. Le vecteur ![]() est colinéaire à
est colinéaire à ![]() donc c’est aussi un vecteur directeur de
donc c’est aussi un vecteur directeur de ![]() .
.
Les coordonnées de ![]() sont :
sont : ![]() . Donc :
. Donc :
- l’abscisse de
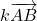 :
: 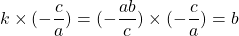 et
et - l’ordonnée de
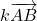 :
: 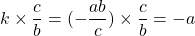
qui sont exactement les coordonnées de ![]() .
.
Les droites ![]() et
et ![]() sont parallèles si et seulement si
sont parallèles si et seulement si ![]()
Démonstration :
1ère partie : Supposons que ![]() . Alors leurs vecteurs directeurs sont colinéaires.
. Alors leurs vecteurs directeurs sont colinéaires.
Un vecteur directeur de ![]() est
est ![]() et un vecteur directeur de
et un vecteur directeur de ![]() est
est ![]() . Si
. Si ![]() et
et ![]() sont colinéaires alors leur déterminant est nul. Ce qui donne :
sont colinéaires alors leur déterminant est nul. Ce qui donne : ![]()
2ème partie (réciproque) : Supposons que ![]() , alors le déterminant de
, alors le déterminant de ![]() et
et ![]() est nul, donc ces deux vecteurs directeurs sont colinéaires. Ce qui permet d’affirmer que les deux droites sont parallèles.
est nul, donc ces deux vecteurs directeurs sont colinéaires. Ce qui permet d’affirmer que les deux droites sont parallèles.
III – Équation cartésienne réduite
Démonstration :
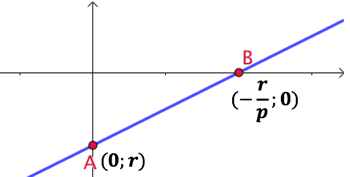 Soit une droite
Soit une droite ![]() dont l’équation cartésienne est
dont l’équation cartésienne est ![]() telle que
telle que ![]() . Alors
. Alors ![]()
Comme ![]() , on peut diviser les deux membres de l’égalité par
, on peut diviser les deux membres de l’égalité par ![]() :
: ![]() , soit
, soit ![]() .
.
En posant ![]() et
et ![]() , on obtient l’équation cartésienne réduite de la droite :
, on obtient l’équation cartésienne réduite de la droite : ![]() .
.
On rappelle que ![]() est le coefficient directeur ou la pente de la droite.
est le coefficient directeur ou la pente de la droite.
Remarque : Si une droite possède une équation cartésienne réduite, celle-ci est unique.
Remarque : On retrouve un résultat déjà rencontré dans le chapitre sur les fonctions affines.
Remarque : On a vu au cours de la démonstration de la propriété précédente, que le cas ![]() correspond à une droite parallèle à l’axe des ordonnées. Ce sont les seules droites qui ne possèdent pas d’équation réduite.
correspond à une droite parallèle à l’axe des ordonnées. Ce sont les seules droites qui ne possèdent pas d’équation réduite.
 Démonstration :
Démonstration :
Si l’équation réduite de ![]() est
est ![]() alors une équation cartésienne de
alors une équation cartésienne de ![]() est
est ![]() . On sait alors qu’un vecteur directeur de
. On sait alors qu’un vecteur directeur de ![]() est
est ![]() .
.
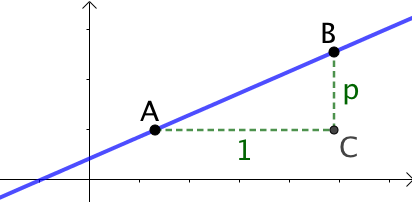
Interprétation : Quand on se déplace sur la droite du point ![]() au point
au point ![]() , d’une distance horizontale égale à
, d’une distance horizontale égale à ![]() , on « monte ou on descend » d’une distance égale à
, on « monte ou on descend » d’une distance égale à ![]() .
.
![]() et
et ![]() sont parallèles si et seulement si elles ont le même coefficient directeur (la même pente), autrement dit : si et seulement si
sont parallèles si et seulement si elles ont le même coefficient directeur (la même pente), autrement dit : si et seulement si ![]() .
.
Démonstration : ![]() et
et ![]() ont comme équations cartésiennes respectives :
ont comme équations cartésiennes respectives : ![]() et
et ![]() .
.
D’après la propriété sur les droites parallèles vue précédemment dans ce chapitre, on sait que ![]() et
et ![]() sont parallèles si et seulement si :
sont parallèles si et seulement si : ![]() ce qui donne
ce qui donne ![]() .
.
IV – Système de deux équations linéaire à deux inconnues
Dans ce paragraphe, ![]() sont des nombres réels donnés. On suppose de plus que
sont des nombres réels donnés. On suppose de plus que ![]() et que
et que ![]()
![]()
Un couple ![]() est solution du système si et seulement si
est solution du système si et seulement si ![]() et
et ![]() vérifient les deux égalités du système.
vérifient les deux égalités du système.
Dans la suite du paragraphe on suppose donné ce système de deux équations linéaires à deux inconnues, que l’on appelle ![]() .
.
1. Résolution géométrique d’un système
La première équation de ![]() peut s’écrire :
peut s’écrire : ![]() . On reconnaît l’équation d’une droite affine
. On reconnaît l’équation d’une droite affine ![]() . Le couple
. Le couple ![]() est solution de cette équation si et seulement si le point
est solution de cette équation si et seulement si le point ![]() appartient à
appartient à ![]() .
.
La seconde équation de ![]() peut s’écrire :
peut s’écrire : ![]() . On reconnaît l’équation d’une droite affine
. On reconnaît l’équation d’une droite affine ![]() . Le couple
. Le couple ![]() est solution de cette équation si et seulement si le point
est solution de cette équation si et seulement si le point ![]() appartient à
appartient à ![]() .
.
Ainsi le couple ![]() est solution du système
est solution du système ![]() si et seulement si le point
si et seulement si le point ![]() est le point d’intersection des droites
est le point d’intersection des droites ![]() et
et ![]() .
.
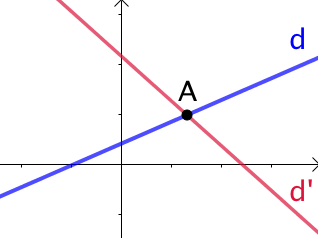
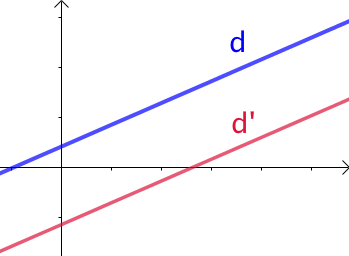
Trois cas sont possibles pour ces deux droites :
 |
 |
 |
2) Résolution algébrique d’un système
Démonstration : La résolution géométrique nous a appris que la condition nécessaire et suffisante pour que ![]() est une solution unique, est que les deux droites ne soient pas parallèles.
est une solution unique, est que les deux droites ne soient pas parallèles.
Nous avons vu dans le chapitre précédent que cette condition est remplie dès lors que ![]() .
.
Il existe une démonstration purement algébrique ne faisant pas appel à la géométrie, qui sera proposée sous forme d’exercice.
Il existe deux méthodes de résolution d’un système de deux équations linéaires à deux inconnues : la méthode par substitution et la méthode par combinaison.
Résoudre un système par la méthode de substitution
Cette méthode est efficace si l’un des coefficients ![]() ou
ou ![]() est égal à 1.
est égal à 1.
Le coefficient devant le ![]() de la première équation est
de la première équation est ![]() . On utilise la méthode de substitution qui consiste à :
. On utilise la méthode de substitution qui consiste à :
- exprimer
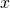 en fonction de
en fonction de 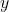 puis
puis - remplacer le
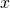 de la seconde équation par l’expression en fonction de
de la seconde équation par l’expression en fonction de 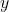 .
.
![]()
De la première équation ![]() , il vient
, il vient ![]() . On remplace ensuite le
. On remplace ensuite le ![]() de la seconde équation par
de la seconde équation par ![]() . Cela donne :
. Cela donne : ![]() .
.
En développant on obtient : ![]() , soit
, soit ![]() , donc
, donc ![]() , soit
, soit ![]() .
.
On revient au premier résultat obtenu qui était : ![]() . Comme nous avons calculé que
. Comme nous avons calculé que ![]() , il vient que
, il vient que ![]() .
.
Conclusion : la solution unique du sytème est le couple : ![]() .
.
Question : sommes-nous certains de notre calcul. Un moyen simple de le confirmer est de remplacer les valeurs trouvées pour ![]() et
et ![]() dans l’une des équations et de vérifier que cette équation est vérifiée. La première équation est
dans l’une des équations et de vérifier que cette équation est vérifiée. La première équation est ![]() .
. ![]() c’est bien le résultat attendu.
c’est bien le résultat attendu.
Question : sommes-nous certains que ![]() est la seule solution possible ? Calculons l’expression
est la seule solution possible ? Calculons l’expression ![]() de ce système :
de ce système : ![]() . Comme on obtient un résultat non nul, nous sommes certains que le système n’a qu’une seule solution.
. Comme on obtient un résultat non nul, nous sommes certains que le système n’a qu’une seule solution.
Résoudre un système par la méthode par combinaison
Cette méthode s’applique si al méthode par substitution n’est pas applicable. Elle consiste à :
- multiplier par un même nombre les deux membres de la première équation ;
- (option) multiplier par un même autre nombre les deux membres de la seconde équation ;
- additionner ou soustraire terme à terme les deux équation pour obtenir une troisième équation où ne subsiste qu’une seule des deux inconnues
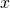 ou
ou 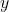 .
.
![]()
On multiplie par ![]() les deux termes de la première équation :
les deux termes de la première équation : ![]() . On obtient :
. On obtient : ![]() .
.
On multiplie par ![]() les deux termes de la première équation :
les deux termes de la première équation : ![]() . On obtient :
. On obtient : ![]() .
.
![]()
On soustrait membre à membre les termes de la seconde équation des termes de la première. Cela donne l’équation : ![]() , soit après simplification :
, soit après simplification : ![]() .
.
On remplace la valeur trouvée pour ![]() dans l’une des deux équation de départ, par exemple la première. On obtient :
dans l’une des deux équation de départ, par exemple la première. On obtient : ![]() , soit
, soit ![]() . Donc
. Donc ![]() .
.
Conclusion : la solution unique du sytème est le couple : ![]()
Deux autres exemples
![]()
Si on multiple par ![]() les deux termes de la première équation, on retrouve exactement la seconde équation.
les deux termes de la première équation, on retrouve exactement la seconde équation.
Cela signifie que le système se résume à une seule de ses deux équations : ![]() par exemple. D’un point de vue géométrique, on a un système de deux équations cartésienne de la même droite.
par exemple. D’un point de vue géométrique, on a un système de deux équations cartésienne de la même droite.
Conclusion : Les solutions du système sont les coordonnées de tous les points de la droite d’équation ![]() .
.
![Rendered by QuickLaTeX.com \[ \text{Résoudre : }\left\{ \begin{array}{rcr} \dfrac{3}{2}x-2y & = & 0 \\ x-\dfrac{4}{3}y & = & 1 \\ \end{array} \right.\]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-d44c532e5acdd8e75e9dab06f5cba97f_l3.png)
Si on multiple les deux termes de la seconde équation par ![]() , on obtient :
, on obtient : ![]() , soit après simplification :
, soit après simplification : ![]()
![Rendered by QuickLaTeX.com \[ \text{Le système s'écrit maintenant : }\left\{ \begin{array}{rcr} \dfrac{3}{2}x-2y & = & 0 \\ \dfrac{3}{2}x-2y & = & \dfrac{3}{2} \\ \end{array} \right.\]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-01f529df62f3109ed6cca78f5f37d2bb_l3.png)
Conclusion : Ce système n’a aucune solution car ![]() .
.
