![]()
Développement limité d’ordre 1 :
![]()
Le DL d’ordre 1 permet de prévoir la position de la courbe par rapport à sa tangente.
Pour ce qui suit, on suppose que ![]() continue sur
continue sur ![]() et dérivable sur
et dérivable sur ![]() .
.
Théorème de Rolle : ![]()
Théorème des accroissements finis : ![]()
Inégalité des accroissements finis :
- Si
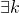 tel que
tel que ![Rendered by QuickLaTeX.com \forall x \in ]a,b[, \lvert f'(x) \rvert \le k](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-0dadfab9362251c99010edf9a7dad170_l3.png) alors
alors 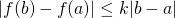
- Si
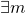 et
et 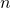 tels que
tels que ![Rendered by QuickLaTeX.com \forall x \in ]a,b[, m \le f'(x) \le M](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-ec6b3b06cea18ed6f07c4c92573212b2_l3.png) , alors
, alors 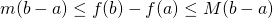
Cette inégalité reste valable pour les fonctions complexes. Faux pour Rolle.
Formule de Leibniz : nième dérivée d’un produit de fonctions
![Rendered by QuickLaTeX.com \[ (fg)^{(n)} = \sum_{k=0}^n \binom{n}{k} f^{(k)} g^{(n-k)} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-14fb1eac6008f722373e6f4cb08943be_l3.png)
DÉRIVÉEES USUELLES
![]()
![]()
![]()
![]()
CONVEXITÉ
![]() convexe sur
convexe sur ![]()
![]() concave
concave ![]() convexe
convexe
![]() convexe sur
convexe sur ![]()
![]() croissante sur
croissante sur ![]() convexe sur
convexe sur ![]() et
et ![]()
![]() sur
sur ![]() convexe
convexe
CALCUL INTÉGRAL ET PRIMITIVES
Dans ce qui suit on suppose que ![]() et
et ![]() sont continues sur
sont continues sur ![]() .
.
![]()
![]()
Inégalité de Cauchy-Schwarz :
![Rendered by QuickLaTeX.com \[ \left \lvert \int_a^b f(t)g(t)dt \right \rvert \le \sqrt{ \int_a^b f(t)^2dt \int_a^b g(t)^2dt} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-40c256fa607f2fb0c03d96cb09799bba_l3.png)
Somme de Riemann
![Rendered by QuickLaTeX.com \[ \text{A gauche : } s_n(f) = \dfrac{b-a}{n} \sum_{k=0}^{n-1} f \left (a + k\dfrac{b-a}{n} \right ) \qquad \qquad \text{A droite : } S_n(f) = \dfrac{b-a}{n} \sum_{k=1}^{n} f \left (a + k\dfrac{b-a}{n} \right ) \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-cdcd34bbb8f4555de917f52d0a77faaa_l3.png)
![]()
![]() continue sur l’intervalle
continue sur l’intervalle ![]() ,
, ![]() et
et ![]() dérivables sur l’intervalle
dérivables sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() . La fonction
. La fonction ![]() définie sur
définie sur ![]() par :
par :
![]()
Quelques méthodes de calcul d’intégrales
Si ![]() est composée de fonctions circulaires, on pose la pseudo fonction
est composée de fonctions circulaires, on pose la pseudo fonction ![]() . Changement de variable à tenter :
. Changement de variable à tenter :
![]()
![]()
![]()
![]()
EQUATIONS DIFFÉRENTIELLES
Premier degré
![]() une primitive de
une primitive de ![]() La solution générale de l’équation homogène :
La solution générale de l’équation homogène : ![]()
Solution particulière de l’équation avec le second membre : on fait varier ![]() .
.
Second degré
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \text{La solution g\'en\'erale de l'\'equation homog\'ene est : } y(x) = \left \lbrace \begin{array}{lr} \lambda e^{r_1 x} + \mu e^{r_2}x & a^2 - 4b > 0 \\ (\lambda x + \mu) e^{rx} & a^2 - 4b = 0 \\ e^{\alpha x} (\lambda \cos (\beta x) + \mu \sin(\beta x)) & a^2 - 4b < 0 \end{array} \right \rbrace (\lambda, \mu) \in \mathbb{R}^2 \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-3a7ce0cfc134c6c8b3cc82670353263c_l3.png)
![Rendered by QuickLaTeX.com \[ \text{Solution particuli\'ere si } f(x) = Ae^{\gamma x} \qquad \left \lbrace \begin{array}{lr} B e^{\gamma x} & \text{ si } \gamma γ \text{ n'est pas solution de l'\'equation caractéristique.} \\ B x e^{\gamma x} & \text{ si } \gamma γ \text{solution simple de l'\'equation caractéristique.} \\ B x^2 e^{\gamma x} & \text{ si } \gamma γ \text{ solution double de l'\'equation caractéristique.} \end{array} \right . \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-f0da27851154ee43edc04824909c8c46_l3.png)
Solution particulière si le second membre est ![]() . On passe aux exponentielles complexes pour revenir au cas précédent, puis on prend la partie réelle ou imaginaire.
. On passe aux exponentielles complexes pour revenir au cas précédent, puis on prend la partie réelle ou imaginaire.