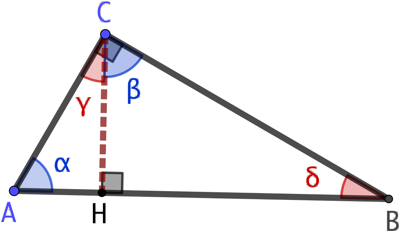
Dans un triangle rectangle, la hauteur issue de l’angle droit découpe ce triangle en deux triangles semblables entre eux et semblables avec le triangle d’origine.
Explications :
Dans le triangle AHC, on a ![]() .
.
Dans le triangle ABC, on a ![]() .
.
Par conséquent ![]() . Ce qui donne :
. Ce qui donne : ![]() .
.
Dans le triangle ABC, on a aussi ![]() . Donc
. Donc ![]() . Ce qui donne :
. Ce qui donne : ![]() .
.
On en conclut que les triangles AHC, HBC et ABC sont semblables.
Remarque : Il s’agit de la proposition VI.8 des Éléments d’Euclide.
