On veut démontrer que les trois hauteurs d’un triangles quelconques sont concourantes.
Construction :
- On construit le triangle ABC;
- On trace ses trois hauteurs (AA’), (BB’) et (CC’);
- On trace la droite (DE) parallèle à (BC) et passant par A;
- On trace la droite (DF) parallèle à (AC) et passant par B;
- On trace la droite (EF) parallèle à (AB) et passant par C.
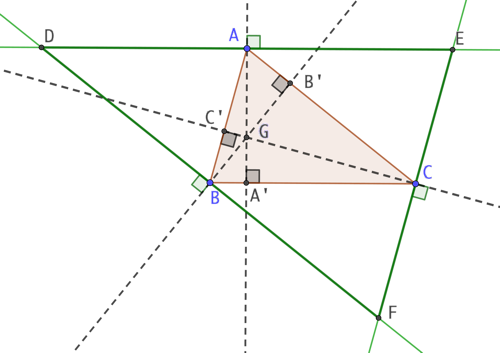Explications :
On va démontrer que les droites (AA’), (BB’) et (CC’) sont les médiatrices du triangle DEF.
Par construction (DE) // (BC) donc (AE) // (BC). De même (EF) // (AB) donc (EC) // (AB).
On en conclut que ABCE est un parallélogramme. On démontre par un raisonnement similaire que ABFC est aussi un parallélogramme. Donc AB =EC = CF, ce qui permet d’affirmer que C est le milieu de [EF].
Par ailleurs, (CC’) étant la hauteur de ABC issue de C, les droites (CC’) et (AB) sont perpendiculaires. Comme (EF) // (AB), on en déduit que (CC’) et (EF) sont perpendiculaires. Or nous avons démontré que C est le milieu de [EF] donc (CC’) est la médiatrice de [EF].
On démontre par un raisonnement similaire que (BB’) est la médiatrice de [DF] et que (AA’) est la médiatrice de [DE]. Or nous savons que les trois médiatrices du triangle DEF sont concourantes en un point G que nous nommons l’orthocentre du triangle. Donc les trois hauteurs du triangle ABC sont concourantes en G.
