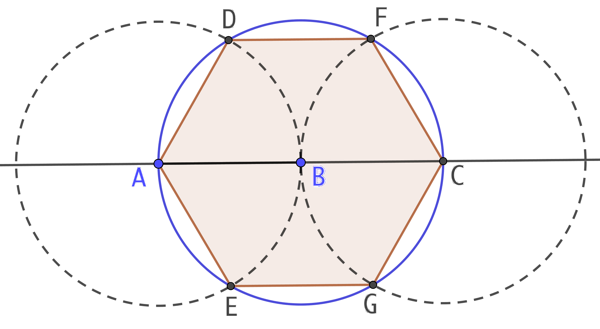
On construit un hexagone de longueur de côté égale à AB ainsi :
- On trace le segment AB.
- On trace le cercle de centre B passant par A.
- On trace la droite (AB) et on place C, le point d’intersection de (AB) avec ce cercle.
- On trace le cercle de centre A passant par B. Ce deuxième cercle coupe le premier cercle aux points D et E.
- On trace le cercle de centre C passant par B. Ce troisième cercle coupe le premier cercle aux points F et G.
- On trace l’hexagone ADFCGE.
 Explications :
Explications :
Les points D, B et E appartiennent au cercle de centre A, donc AD = AB = AE.
De même les points F, B et G appartiennent au cercle de centre C, donc CF = CB = CG.
Les points A et C appartiennent au cercle de centre B, donc AB = CB.
De toutes ces égalités il vient : AD = AE = CF = CG = AB. À présent on sait que 4 des 6 côtés du polygone ADFCGE ont la même longueur. Restent à traiter les côtés DF et EG.
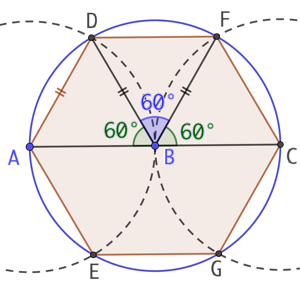
On sait que ABD et BCF sont deux triangles équilatéraux dont les côtés ont tous comme longueur AB. Pour s’en persuader voir : Triangle équilatéral. Puisque BD = BF, on peut déjà affirmer que BFD est un triangle isocèle en B.
Nous avons l’égalité des mesures d’angles : CBF + FBD + DBA = 180°. Comme ABD et BCF sont deux triangles équilatéraux, les angles CBF et DBA mesurent chacun 60°. Il vient donc que l’angle FBD mesure aussi 60°. Alors si BFD est un triangle isocèle dont l’un des angles mesure 60°, c’est un triangle équilatéral. On en conclut que DF = DB = DA.
On démontrerait de la même manière que EG = EA. Par conséquent les 6 côtés du polygone ADFCGE sont de même longueur, il s’agit donc d’un hexagone.
