![]() .
.
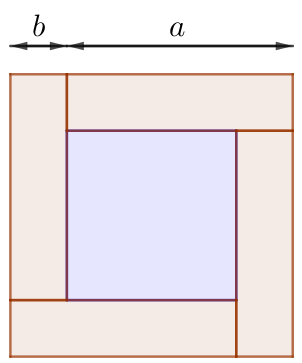
la somme des aires des 4 rectangles de côtés ![]() et
et ![]() est égale à la différence entre l’aire du carré de côté
est égale à la différence entre l’aire du carré de côté ![]() et l’aire du carré de côté
et l’aire du carré de côté ![]() .
.
La preuve algébrique est évidente en partant des deux identités remarquables bien connues :
![]()
Ce qui est affirmé sans preuve peut être nié sans preuve (Euclide). Le but ultime n'est rien, le mouvement est tout (Eduard Bernstein)


![]() .
.
la somme des aires des 4 rectangles de côtés ![]() et
et ![]() est égale à la différence entre l’aire du carré de côté
est égale à la différence entre l’aire du carré de côté ![]() et l’aire du carré de côté
et l’aire du carré de côté ![]() .
.
La preuve algébrique est évidente en partant des deux identités remarquables bien connues :
![]()