La somme des longueurs de deux côtés quelconques d’un triangle est supérieur à la longueur du troisième côté.
Explications :
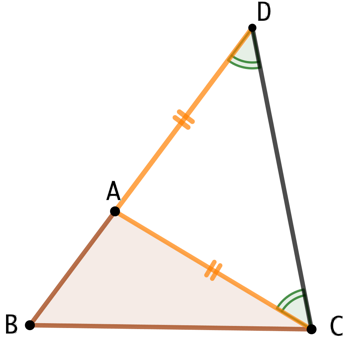
Soit un triangle ABC pour lequel [BC] est le côté le plus long. On prolonge le segment [BA] par un segment [AD] dont la longueur est égale à celle de [AC]. On obtient ainsi un triangle DAC isocèle en A.
Par conséquent 
.
Comme 
et 
, il vient que 
.
Puisqu’à un grand angle correspond un grand côté, on peut conclure que BC < BD, soit BC < AB + AC.
Remarque : Il s’agit de la proposition n°I.20 des Éléments d’Euclide.
