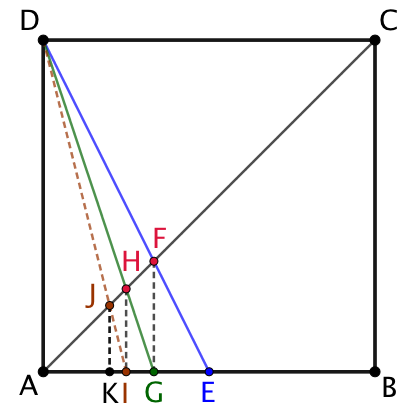
Inverse des nombres entiers par Thales

Étant donné un carré d’une unité de côté, on peut déterminera les valeurs des inverses des nombres entiers avec le théorème de Thalès.

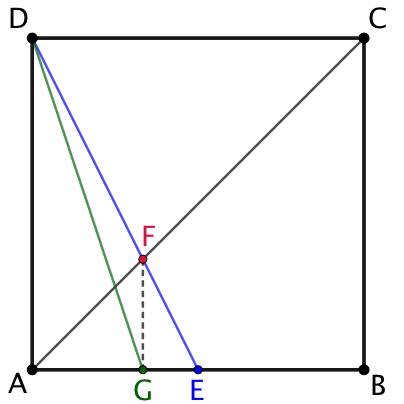Construction :

  • Soit E le milieu de [AB]. alors AE = \dfrac{1}{2}.
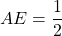  • [DE] coupe la diagonale [AC] en F. Soit G le projeté orthogonal de F sur (AB). Alors AG = \dfrac{1}{3}.
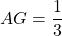  • [DG] coupe la diagonale [AC] en H. Soit I le projeté orthogonal de H sur (AB). Alors AI = \dfrac{1}{4}.
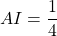  • et ainsi de suite…

Explications :

[AC] est une diagonale du carré ABCD donc le triangle AGF est isocèle et rectangle en G donc FG = AG.

On applique le théorème de Thales dans le triangle DAE : \dfrac{FG}{DA} = \dfrac{EG}{EA}. Par ailleurs DA = 1 et EA = 0,5

Ce qui donne : \dfrac{AG}{1} = \dfrac{EG}{0,5} soit EG = 0,5 \times AG.

AG + GE = AG + 0,5 \times AG = 1,5 \times AG. Comme AG + GE = AE = 0,5, il vient que 1,5 \times AG = 0,5. Donc AG = \dfrac{1}{3}

Print Friendly, PDF & Email