Inverse d’un nombre

On construit l’inverse d’un nombre a ainsi :

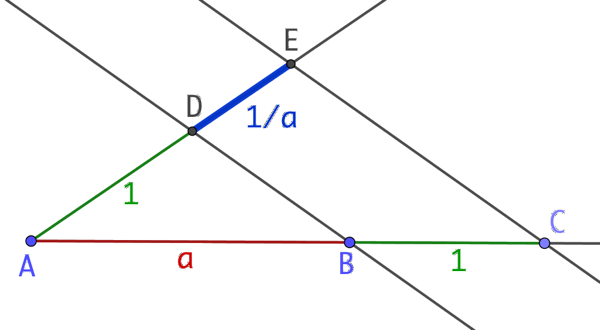
1. On trace une demi-droite issue d’un point A.
2. On place sur cette droite le point B tel que AB = a et le point C tel que BC = 1.
3. On trace une seconde droite sécante en A à la première droite.
4. On place sur cette droite le point D tel que AD = 1.
5. On trace la droite (BD) et la droite parallèle à (BD) passant par C.
6. Cette parallèle coupe la droite (AD) au point E. La longueur du segment [DE] vaut l’inverse de a.

Explications :

On utilise le théorème de Thales : Etant donné que les droites (BD) et (CE) sont parallèles, on peut écrire l’égalité des rapports suivants : . En remplaçant par les valeurs, on obtient : , d’où .