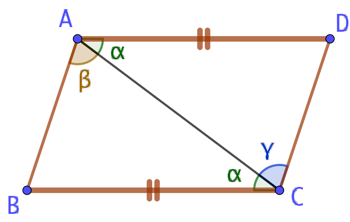
C’est ainsi qu’Euclide, dans ses « Éléments », introduit la notion de parallélogramme : Étant donnés deux segments [AD] et [BC] de même longueur et portés par deux droites parallèles, les droites (AB) et (DC) sont parallèles et les segments [AB] et [DC] sont de même longueur.
Explications :
On trace la droite (AC). (AD) et (BC) sont parallèles donc les angles alternes-internes qu’elles forment avec la sécante (AC) sont de même mesure 
.
Les triangles ACD et ABC ont un côté commun, AC, et deux côtés de même longueur : BC et AD. Par ailleurs les angles situés entre ces côtés deux à deux égaux (). Donc les deux triangles sont isométriques et leurs trois angles sont deux à deux égaux. En particulier, nous avons 
. Ce qui permet de conclure que les droites (AB) et (DC) sont parallèles puisqu’elles forment avec (AC) deux angles alternes-internes de même mesure.
Enfin, puisque les deux triangles sont isométriques, leurs côtés AB et CD sont de même longueur.
Remarque : Il s’agit de la proposition I.33 des Éléments d’Euclide. La proposition I.34 est très proche. Elle précise que la diagonale d’un parallélogramme le divise en deux triangles isométriques.
