I – Description d’un parallélépipède rectangle
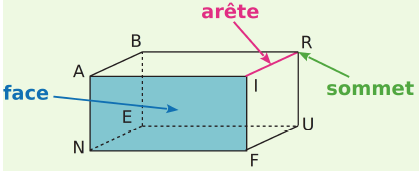Exemple : Cette figure représente le parallélépipède rectangle ABRINEUF en perspective cavalière.
- Le point R est un sommet.
- Le segment [RI] est une arête.
- Le rectangle NAIF délimite une face.
Remarque : Un cube est un pavé droit particulier dont les six faces sont des carrés superposables.
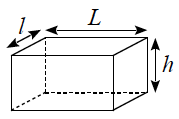Un parallélépipède rectangle a 8 sommets, 12 arêtes et 6 faces.- Un parallélépipède est défini par trois dimensions : sa longueur, sa largeur et sa hauteur.
- Pour un cube, la longueur, la largeur et la hauteur sont égales.
II – Représentation en perspective cavalière
En perspective cavalière :
- les figures face à l’observateur sont dessinées en vraie grandeur sans déformation ;
- les droites parallèles en réalité le sont sur le dessin ;
- les arêtes cachées sont dessinées en pointillés.
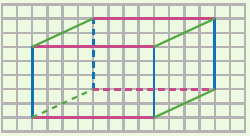
Étapes pour représenter un pavé droit en perspective cavalière :
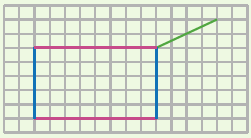
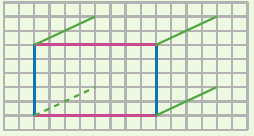
| On commence par la face avant en vraie grandeur. | On trace les arêtes transversales, parallèles et de même longueur, mais pas en vraie grandeur. | On finit par la face arrière, en vraie grandeur. |
 |
 |
 |
III – Patron d’un parallélépipède rectangle
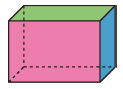Il existe plusieurs patrons différents permettant de le construire ce pavé droit. Les faces de la même couleur sur chaque patron sont superposables et représentent, pour le pavé droit, des faces parallèles.
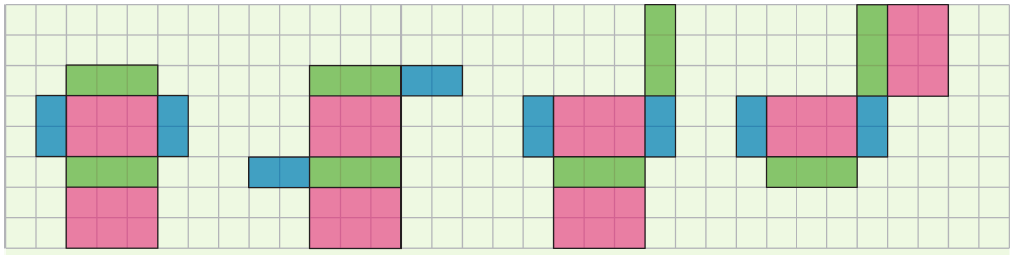
Remarque : Il existe beaucoup d’autres patrons du pavé droit. Pour le cube, il existe 11 patrons différents.
IV – Volume d’un parallélépipède rectangle
ATTENTION : Pour calculer un volume, les dimensions doivent être exprimées dans la même unité de longueur.
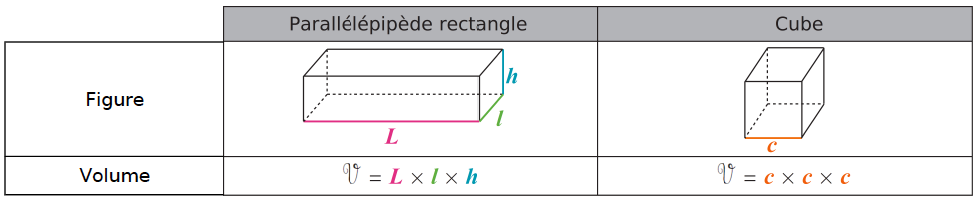
Exemple : Calcule le volume d’un pavé droit de 32 mm de longueur, 2,5 cm de largeur et 0,4 dm de hauteur.
- On écrit la formule :
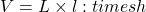
- On remplace par les données numériques exprimées dans la même unité : 32 mm = 3,2 cm et 0,4 dm = 4 cm.
- Le volume du pavé droit est
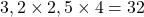cm3.
Exemple : Calcule le volume d’un cube de 5,3 cm de côté.
cm3
