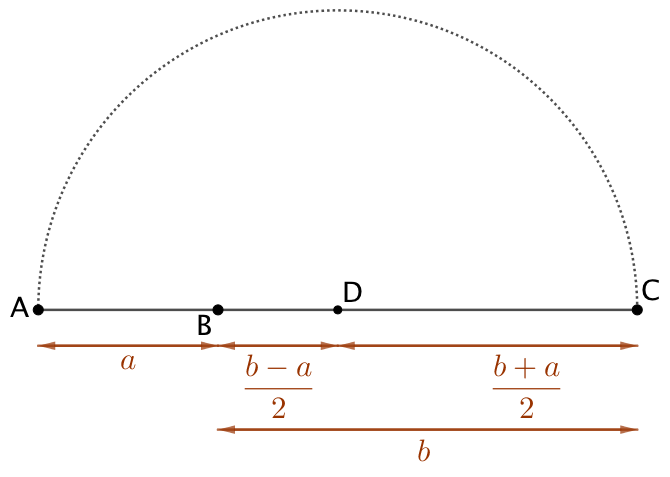
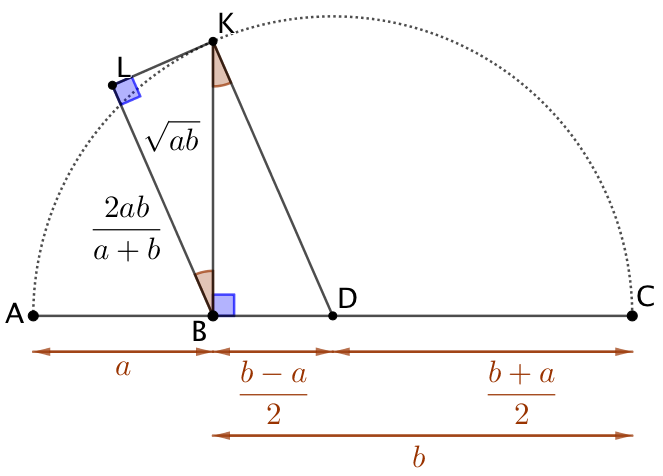
Les 4 moyennes : arithmétique, géométrique, harmonique et quadratique (Version 2)


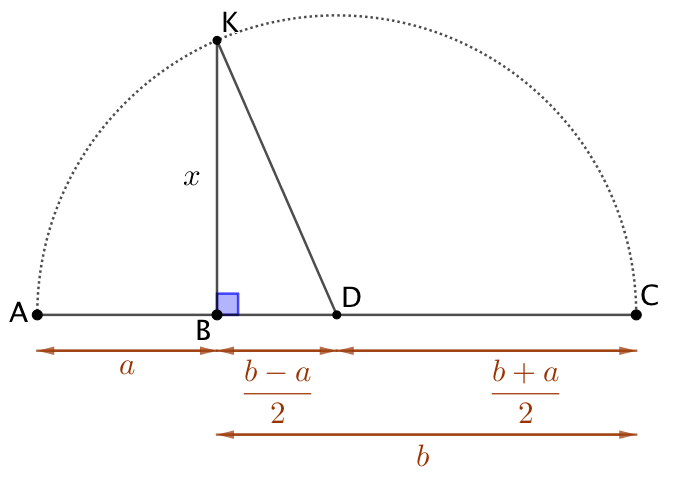
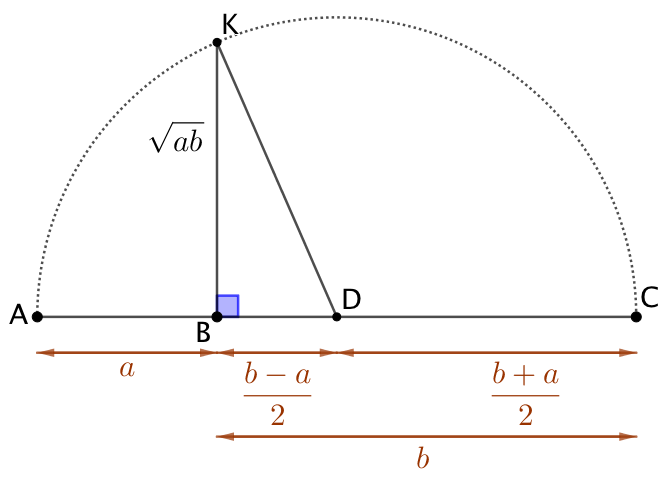
Moyenne arithmétique : $\dfrac{a+b}{2}$	$x^2 = \left ( \dfrac{a+b}{2} \right ) ^2 - \left ( \dfrac{b-a}{2} \right ) ^2$	Moyenne géométrique : $x = \sqrt{ab}$

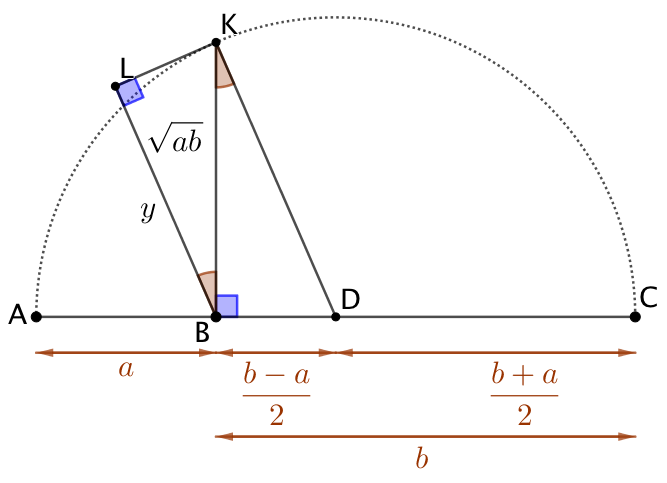
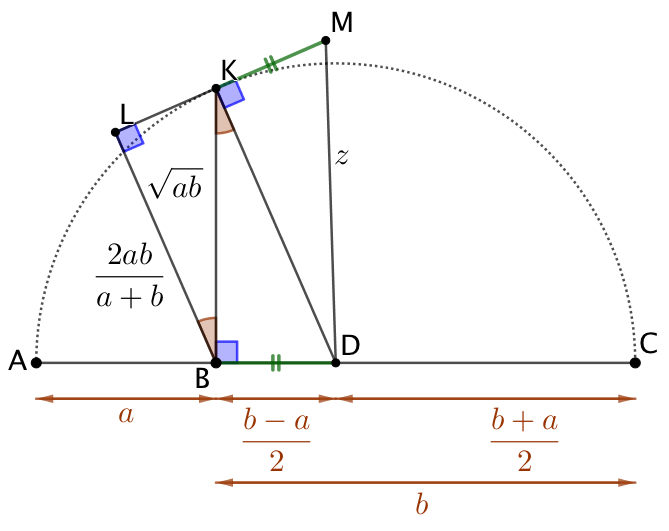
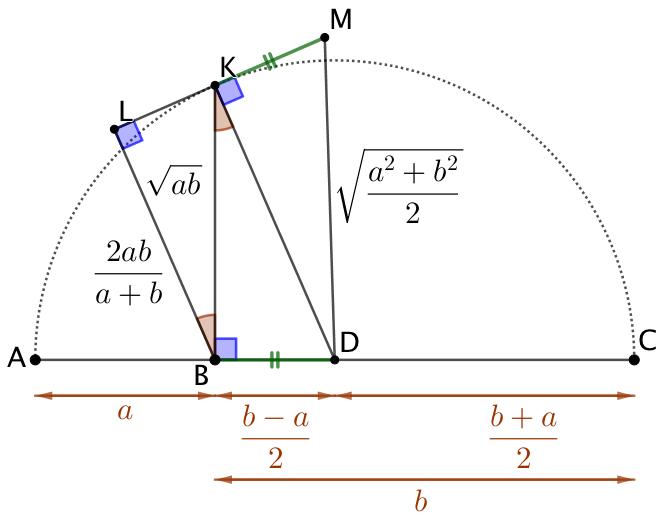$(BL) \parallel (DK)$ et $(BL) \perp (LK)$ $\widehat{KBL} = \widehat{BKD}$ $\dfrac{y}{BK} = \dfrac{BK}{DK} \implies y = \dfrac{BK^2}{DK}$	Moyenne harmonique : $y = \dfrac{2ab}{a+b}$	$KM = BD$ et $(KM) \perp (KD)$ $z^2 = \left ( \dfrac{a+b}{2} \right ) ^2 + \left ( \dfrac{b-a}{2} \right ) ^2 = \dfrac{a^2 + b^2}{2}$
	Moyenne quadratique : $z = \sqrt{ \dfrac{a^2 + b^2}{2}}$	On observe que $DM \ge DK \ge BK \ge BL$ . Donc les moyennes classées dans l’ordre décroissant sont : la moyenne quadratique la moyenne arithmétique la moyenne géométrique la moyenne harmonique