I – Les entiers naturels
![]()
- On emploie le signe
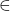 pour indiquer qu’un nombre appartient à un ensemble.
pour indiquer qu’un nombre appartient à un ensemble. - On emploie le signe
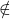 pour indiquer qu’un nombre n’appartient pas à un ensemble.
pour indiquer qu’un nombre n’appartient pas à un ensemble.
Exemple : ![]() mais
mais ![]() .
.
On dit aussi que ![]() est divisible par
est divisible par ![]() ou que
ou que ![]() est un multiple de
est un multiple de ![]() (ou encore que
(ou encore que ![]() divise
divise ![]() ).
).
Exemple : ![]() est un multiple de
est un multiple de ![]() car
car ![]() .
. ![]() est aussi un multiple de
est aussi un multiple de ![]() .
.
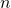 est pair si et seulement s’il existe
est pair si et seulement s’il existe 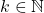 tel que
tel que 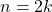 .
.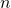 est pair si et seulement s’il existe
est pair si et seulement s’il existe 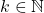 tel que
tel que 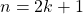 .
.
Démonstration : Soient ![]() et
et ![]() deux multiples de
deux multiples de ![]() .
.
Alors il existe deux entiers ![]() et
et ![]() tels que :
tels que : ![]() et
et ![]() .
.
![]() . Ce qui démontre que
. Ce qui démontre que ![]() et un multiple de
et un multiple de ![]() .
.
On démontre de façon similaire que ![]() est aussi un multiple de
est aussi un multiple de ![]() .
.
- Le carré d’un nombre pair est pair.
- Le carré d’un nombre impair est impair.
Démonstration : Soit ![]() et supposons que
et supposons que ![]() est impair.
est impair.
Alors il existe ![]() tel que
tel que ![]() .
.
![]() . Donc
. Donc ![]() est la somme d’un multiple de 2 et 1. Cela démontre que
est la somme d’un multiple de 2 et 1. Cela démontre que ![]() est impair.
est impair.
On démontre de façon similaire que le carré d’un nombre pair est pair.
II – Les entiers relatifs
![]()
Remarque : Z est la première lettre du verbe allemand Zählen qui signifie compter.
Les nombres négatifs permettent, par exemples, des calculs de gains et de pertes. Ils servent également à se repérer sur un droite, un plan ou dans l’espace à trois dimensions, par rapport à une origine.
III – Les nombres décimaux
- L’ensemble des nombres décimaux, noté
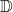 , est l’ensemble des nombres pouvant s’écrire sous la forme d’une fraction dont le dénominateur est une puissance de 10.
, est l’ensemble des nombres pouvant s’écrire sous la forme d’une fraction dont le dénominateur est une puissance de 10. - Autrement dit : un nombre est décimal s’il peut s’écrire sous la forme
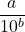 , où
, où 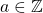 et
et 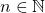 .
. - Ce sont les nombres négatifs ou positifs possédant un nombre fini de chiffres après la virgule.
Exemple : ![]() .
.
Les nombres décimaux permettent de diviser une unité en sous-unités : les dixièmes, les centièmes,… afin d’être plus précis dans les calculs ou dans les repérages dans l’espace.
IV – Les nombres rationnels
- L’ensemble des nombres rationnels, noté
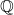 , est l’ensemble des nombres pouvant s’écrire sous la forme d’une fraction.
, est l’ensemble des nombres pouvant s’écrire sous la forme d’une fraction. - Autrement dit : un nombre est rationnel s’il peut s’écrire sous la forme
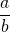 , où
, où 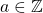 et
et 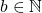 ..
..
Etymologie : Rationnel dans le sens « ratio », proportion en anglais, qui vient du latin « ratio » signifiant calcul et qu’on retrouve en français avec le mot ration.
Exemples :
L’écriture sous décimale d’un nombre rationnel est toujours périodique.
Les nombres rationnels permettent de traduire en nombres la notion de partage, quelque soit le dénominateur.
Exemple : 14 et 15 sont premiers entre eux. Car :
- les diviseurs de 14 sont : 1 ; 2 ; 7 et 14.
- les diviseurs de 15 sont : 1 ; 3 ; 5, et 15.
Simplifier une fraction c’est trouver une fraction irréductible qui lui soit égale. La méthode consiste à déterminer les décompositions en facteurs premiers du numérateur et du dénominateur.
Exemple : Simplifions ![]()
On sait déjà que ![]()
![]()
![]()
V – Les nombres réels
Il s’agit de l’ensemble de tous les nombres possibles y compris ceux qui ne peuvent pas s’écrire sous la forme d’une fraction, et que l’on appelle les nombres irrationnels.Cet ensemble est noté noté ![]() .
.
Exemples : ![]()
Ainsi nous avons les relations suivantes : ![]() .
.
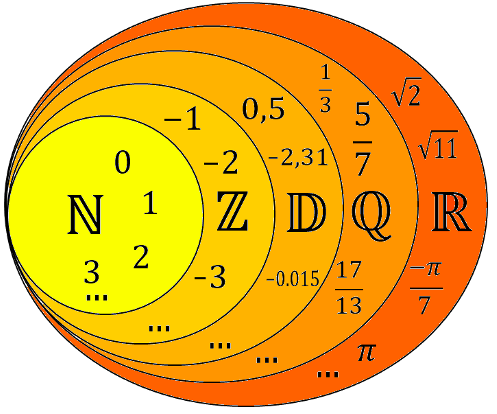 Cela signifie que
Cela signifie que
- tous les entiers naturels sont aussi des entiers relatifs qui sont eux-même des nombres décimaux qui sont des nombres rationnels qui sont des nombres réels ;
- Un même nombre admet plusieurs écritures différentes. Par exemple le nombre 2 peut aussi s’écrire :
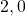 ou
ou  ou
ou  ou
ou 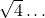 .
.
L’arithmétique nous permet de démontrer que la racine de 2 ne peut être un nombre rationnel. Pour cela on utilise un raisonnement par l’absurde qui consiste à supposer le contraire de ce qu’on veut démontrer pour arriver à une contradiction qui permet alors d’affirmer que notre supposition était fausse et que son contraire est par conséquent vrai.
Supposons donc que ![]() est un nombre rationnel. Alors il existe
est un nombre rationnel. Alors il existe ![]() et
et ![]() , tels que
, tels que ![]() . On suppose de plus que la fraction
. On suppose de plus que la fraction ![]() est irrationnelle, donc que
est irrationnelle, donc que ![]() et
et ![]() sont premiers entre eux.
sont premiers entre eux.
Alors ![]() , soit
, soit ![]() .
.
Donc ![]() , ce qui implique que
, ce qui implique que ![]() est un nombre pair, donc que
est un nombre pair, donc que ![]() est un nombre pair. Si
est un nombre pair. Si ![]() était impair, alors une propriété précédente nous apprend que
était impair, alors une propriété précédente nous apprend que ![]() serait aussi impair, or nous savons que
serait aussi impair, or nous savons que ![]() est pair.
est pair.
Si ![]() est pair, il existe
est pair, il existe ![]() , tel que
, tel que ![]() , ce qui donne
, ce qui donne ![]() .
.
On sait ![]() donc
donc ![]() , ce qui donne
, ce qui donne ![]() . Ce qui implique que
. Ce qui implique que ![]() est pair, donc que
est pair, donc que ![]() est pair.
est pair.
Nous venons d’arriver à la conclusion que ![]() et
et ![]() sont pairs, donc divisibles par 2. Donc ils ne sont pas premiers entre eux. Or nous avions supposés qu’ils étaient premiers entre eux !
sont pairs, donc divisibles par 2. Donc ils ne sont pas premiers entre eux. Or nous avions supposés qu’ils étaient premiers entre eux !
Nous aboutissons à une contradiction dans notre raisonnement. Notre supposition était fausse et le nombre ![]() est irrationnel.
est irrationnel.
VI – Droite numérique
- un point O appelé origine de la droite graduée ;
- une unité.
- Tout point d’une droite graduée peut être repéré par un nombre réel unique appelé son abscisse.
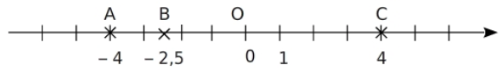 Exemple :
Exemple :
- L’abscisse de l’origine O est le nombre 0.
- Les points A, B et C ont pour abscisses respectives
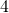 ;
; 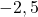 et
et 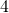 .
.
On note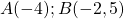 et
et 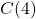 .
.
VII – Intervalles
Soient deux réels ![]() et
et ![]() tels que
tels que ![]() .
.
| L’intervalles des réels |
est noté | et est représenté sur la droite numérique par |
|
 |
|
|
 |
|
|
 |
|
|
 |
![]() se lit « plus l’infini », c’est-à-dire vers les plus grands nombres.
se lit « plus l’infini », c’est-à-dire vers les plus grands nombres. ![]() se lit « moins l’infini », c’est-à-dire vers les plus petits nombres.
se lit « moins l’infini », c’est-à-dire vers les plus petits nombres.
VIII – Valeur absolue
Si ![]()
Si ![]()
![]()
 Exemples :
Exemples :
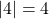 . C’est la distance OA.
. C’est la distance OA.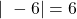 . C’est la distance OB.
. C’est la distance OB.
Démonstration : Soit ![]()
Si ![]() alors
alors ![]() , donc
, donc ![]() .
.
Si ![]() alors
alors ![]() , donc
, donc ![]() .
.
Démonstration : ![]() . Donc
. Donc ![]() et
et ![]() sont opposés. Alors ils ont la même valeur absolue.
sont opposés. Alors ils ont la même valeur absolue.
 Exemple : Soient les points
Exemple : Soient les points ![]() et
et ![]() .
.
![]()
![]() ou
ou
![]() .
.
Démonstration :
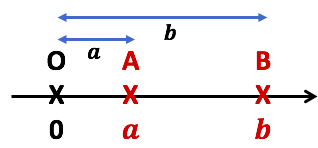 1er cas :
1er cas : ![]()
Comme ![]() alors
alors ![]() , donc
, donc ![]()
![]() .
.
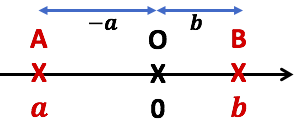 2ème cas :
2ème cas : ![]()
Comme ![]() alors
alors ![]() , donc
, donc ![]()
![]()
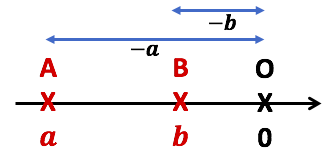
3ème cas : ![]()
Comme ![]() alors
alors ![]() , donc
, donc ![]()
![]()
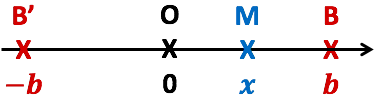 La figure de droite décrit la situation de cette propriété :
La figure de droite décrit la situation de cette propriété :
- 2 points
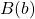 et
et 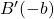 sont symétriques par rapport à l’origine O et
sont symétriques par rapport à l’origine O et - un point
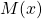 est situé entre B et B’.
est situé entre B et B’. - La distance OM est nécessairement inférieur à OB, c’est-à-dire que
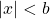 .
.
Démonstration :
1ère partie : Supposons que ![]() , c’est-à-dire que
, c’est-à-dire que ![]() .
.
Cas n°1 : ![]() alors
alors ![]() . Si
. Si ![]() alors
alors ![]()
Cas n°2 : ![]() alors
alors ![]() . Si
. Si ![]() alors
alors ![]() . Donc
. Donc ![]() .
.
2ème partie (réciproque) : Supposons que ![]() .
.
Cas n°1 : ![]() alors
alors ![]() . Donc
. Donc ![]() .
.
![]() donc
donc ![]() . Comme
. Comme ![]() , nécessairement
, nécessairement ![]() . On en conclut que
. On en conclut que ![]() , c’est-à-dire que
, c’est-à-dire que ![]() .
.
Cas n°2 : ![]() alors
alors ![]() , donc
, donc ![]() , ce qui donne
, ce qui donne ![]() .
.
Étant donné que ![]() et que
et que ![]() , nécessairement
, nécessairement ![]() . On en conclut que
. On en conclut que ![]() , c’est-à-dire que
, c’est-à-dire que ![]() .
.
IX – Valeur approchée
Exemple : ![]()
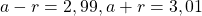 . On a bien
. On a bien ![Rendered by QuickLaTeX.com 3,004 \in [2,99 ; 3,01]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-035b3df782e9bd8ed444f8f3f2f23d55_l3.png) et
et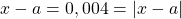 . On a bien
. On a bien 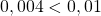
Démonstration :
1ère partie : Supposons que ![]() .
.
Cela signifie que ![]() , c’est-à-dire :
, c’est-à-dire : ![]() et
et ![]() .
.
![]() donne
donne ![]() .
. ![]() donne
donne ![]() .
.
Donc nous avons obtenu : ![]() . On en conclut que
. On en conclut que ![]() .
.
2ème partie (réciproque) : Supposons que ![]() .
.
Cela signifie que ![]() , c’est-à-dire :
, c’est-à-dire : ![]() et
et ![]() .
.
Si ![]() alors
alors ![]() . Si
. Si ![]() alors
alors ![]() .
.
On obtient donc ![]() , soit
, soit ![]() .
.
Exemples :
La distance Terre-Lune est de 384 399 km. 384 000 km représente une valeur approchée de cette distance à ![]() près. Car
près. Car ![]() et
et ![]() .
.
La valeur de ![]() qui intervient dans le calcul du périmètre d’un cercle est 3.141 592 653 59 … La valeur approchée de
qui intervient dans le calcul du périmètre d’un cercle est 3.141 592 653 59 … La valeur approchée de ![]() à
à ![]() près est bien connue :
près est bien connue : ![]() .
.
EXERCICES
5 pages d’exercices corrigés à télécharger :
- Démontrer par l’absurde que
 n’est pas un nombre décimal.
n’est pas un nombre décimal. - 1 / 15 : trouver l’abscisse de points
- 2 / 15 : plus petit ensemble de nombres
- 4 / 15 : à quel ensemble appartient un nombre ?
- 6 / 15 : un nombre est-il décimal ?
- 7 / 15 : vrai ou faux sur des opérations de nombres
- 8 / 15 : mauvais raisonnement
- 13 / 15 : chercher deux nombres irrationnels dont le produit est un entier
- 14 / 17 : dessiner des intervalles sur une droite et vis-versa
- 15 / 17 : appartenance d’un nombre à un intervalle
- 16 / 17 : comprendre les intervalles
- 20 / 18 : inégalités et intervalles
- 22 / 18 : nombre égal à sa valeur absolue ?
- 24 / 18 : calcul de valeurs absolues
- 25 / 18 : distance entre deux nombres
- 26 / 18 : 2 solution de l’inégalité avec valeur absolue ?
- 27 / 18 : résoudre des équations avec valeur absolue
- 28 / 18 : vrai ou faux sur les valeurs absolues
- 30 / 18 : encadrement
- 48 / 21 : comparaison de fractions
- 50 / 21 : calcul littéral avec fractions
- 121 / 29 : démonstration sur les nombres impairs
- 127 / 32 : sommes de 3 nombres consécutifs
