Les nombres décimaux – Deuxième partie

I – Addition et soustraction de nombres décimaux

Règle
Pour poser et effectuer une addition ou une soustraction de nombres décimaux, on place les nombres les uns en dessous des autres, de sorte que les virgules soient alignées verticalement. Ensuite, on utilise les règles de l’addition et de la soustraction des nombres entiers, en n’oubliant pas à la fin de placer la virgule, si nécessaire.

Cette addition est mal posée car le nombre 84, qui n’a pas de virgule, devrait être placé sous la partie entière de 12,7. Cette addiction est correctement posée.

 

Pour poser la soustraction 12 – 6,7, on place les nombres correctement et on ajoute un zéro pour que les deux nombres aient le même nombre de chiffres dans leurs parties décimales (en effet, 12 = 12,0).

II – Multiplication et division par 10 ; 100 ; 1000 …

Pour multiplier par On décale la virgule vers la droite. Si nécessaire on ajoute des zéros à droite Exemples
10 1 rang vers la droite 0,47 \times 10 = 4,7

47 \times 10 = 470
100 2 rangs vers la droite 3,14 \times 100 = 314

0,7 \times 100 = 70
1000 3 rangs vers la droite 9,2145 \times 1000 = 9214,5

9,81 \times 1000 = 9810

 

Pour diviser par On décale la virgule vers la gauche. Si nécessaire on ajoute des zéros à gauche Exemples
10 1 rang vers la gauche 27,1 \div 10 = 2,71

47 \div 10 = 4,7

7 \div 10 = 0,7
100 2 rangs vers la gauche 456,5 \div 100 = 4,565

710 \div 100 = 7,10 = 7,1

13 \div 100 = 0,13

3 \div 100 = 0,03
1000 3 rangs vers la gauche 3719,2 \div 1000 = 3,7192

1234 \div 1000 = 1,234

123 \div 1000 = 0,123

0,3 \div 1 000 = 0,0003

III – Multiplication par 0,1 ; 0,01 ; 0,001

Multiplier par C’est diviser par Exemples
0,1 10 car 0,1 = \dfrac{1}{10} 78 x 0,1 = 7,8
0,01 100 car 0,01 = \dfrac{1}{100} 3,5 × 0,01 = 003,5 × 0,01 = 0,035
0,001 1000 car 0,001 = \dfrac{1}{1000} 56,2 × 0,001 = 0056,2 × 0,001 = 0,0562

IV – Conversion des unités de longueur et de masse

1) Unités de longueur

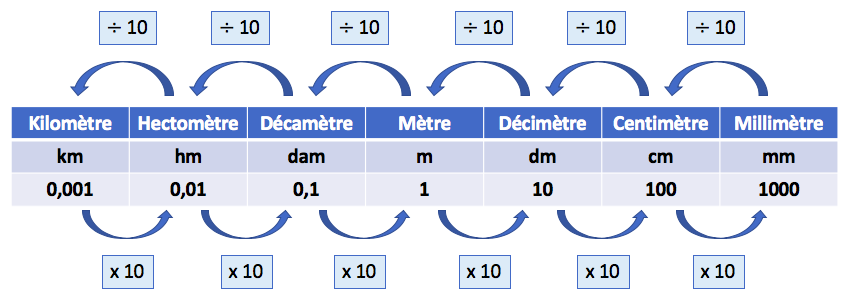
Exemples :

  • 1 km = 1000 m = 100 000 cm
  • 1 mm = 0,01 dm

Fractions de longueurs :

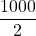  • Un demi kilomètre, c’est \dfrac{1}{2} km. C’est aussi \dfrac{1000}{2} m, soit 500 m.
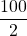  • Un quart de mètre, c’est \dfrac{1}{4} m. C’est aussi \dfrac{100}{2} cm, soit 25 cm.

2) Unités de masse

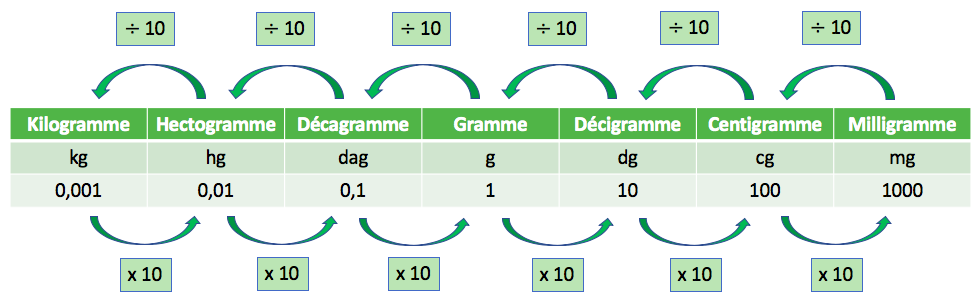
Exemples :

  • 1 kg = 100 dag = 1000 g = 1 000 000 mg
  • 1 dg = 0,1 g = 0,01 hg

Remarque : On utilise également d’autres unités de masse :

  • le quintal (q) qui équivaut à 100 kg : 1 q = 100 kg ;
  • la tonne (t) qui équivaut à 1 000 kg : 1 t = 1 000 kg.

Fractions de masses :

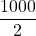  • Un demi kilogramme, c’est \dfrac{1}{2} kg. C’est aussi \dfrac{1000}{2} g, soit 500g.
  • Un quart de décigramme, c’est \dfrac{1}{4} dg. C’est aussi 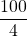\dfrac{100}{4} mg, soit 25 mg.

V – Multiplication de deux nombres décimaux

Règle
Pour effectuer la multiplication de deux nombres décimaux,

  • on effectue d’abord la multiplication sans tenir compte des virgules ;
  • on place la virgule dans le produit en utilisant la méthode décrite dans l’exemple.

Exemple : On veut effectuer la multiplication de 2,34 par 1,2.

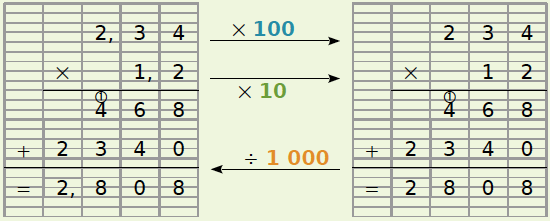234 est 100 fois plus grand que 2,34 et 12 est 10 fois plus grand que 1,2.

Le produit 2,34 x 1,2 est donc 1 000 fois plus petit que 2 808.

Finalement 2,34 × 1,2 = 2,808.

 

 

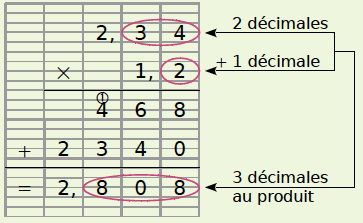Le facteur 2,34 a deux chiffres après la virgule.

Le facteur 1,2 a un chiffre après la virgule.

On doit donc placer la virgule dans le produit de telle sorte qu’il y ait 2 + 1 = 3 chiffres après la virgule.

 

Propriété : Priorité de la multiplication
Si on doit réaliser une série d’opérations comportant des additions et des multiplications, on commence par effectuer les multiplications puis on effectue les additions.

Exemple : 7,1 x 3 + 6 x 5,4.

  • On calcule les produits : 7,1 x 3 = 21,3 et 6 x 5,4 = 32,4
  • Puis on fait la somme des produits : 21,3 + 32,4 = 53,7

3) Multiplications particulières

Règle
  • Multiplier un nombre par 0,5 est équivalent à la diviser par deux.
  • Multiplier un nombre par 0,25 est équivalent à le diviser par quatre.

Exemples :

    \[ 80 \times 0,5 = 40 \qquad 40 \times 0,25 = 10 \qquad 53 \times 0,1 = 5,3 \]

VI – Division d’un nombre décimal par un nombre entier

Règle
Effectuer la division décimale de deux nombres, c’est trouver la valeur exacte ou une valeur approchée du quotient de ces deux nombres.

Exemples : On va effectuer la division de 75,8 par 4 puis celle de 4,9 par 9.

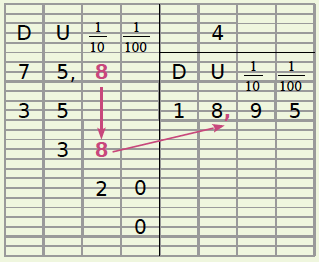Dès que l’on abaisse le chiffre des dixièmes du dividende, on place la virgule dans le quotient.

 

Le nombre 18,95 est la valeur exacte du quotient de 75,8 par 4.

 

 

 

 

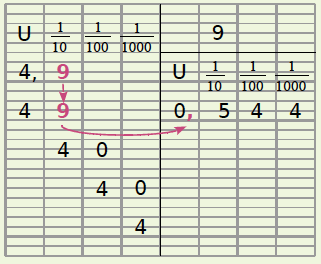Le nombre 0,544 est une valeur approchée au millième du quotient de 4,9 par 9.

Print Friendly, PDF & Email