I – Écritures des nombres
Exemples :
- 1 054 est un nombre de quatre chiffres.
- 7 est un nombre d’un seul chiffre.
Exemple : 1049658723 s’écrit 1 049 658 723.
On peut utiliser un tableau comme celui-ci :
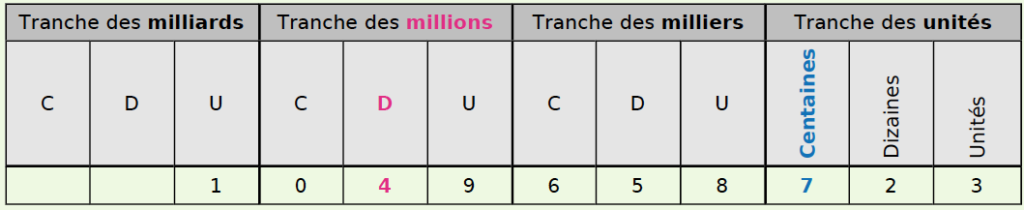
Ce nombre s’écrit : un-milliard-quarante-neuf-millions-six-cent-cinquante-huit-mille-sept-cent-vingt-trois.
Il se décompose ainsi :
1 049 658 723 = (1 x 1 000 000 000) + (4 x 10 000 000) + (9 x 1 000 000) + (6 x 100 000) + (5 x 10 000) + (8 x 1 000) + (7 x 100) + (2 x 10) + (3 x 1).
7 est le chiffre des centaines et 4 est le chiffre des dizaines de millions.
Le nombre de millions est 1 049. À ne pas confondre avec le chiffre des millions qui est 9.
| Vidéo sur l’écriture et la décomposition des nombres entiers |
II – Repérage sur une demi-droite graduée
Exemple : Quelles sont les abscisses des points A et B ?
Le point A a pour abscisse 300. On note A(300). B est le point d’abscisse 800. On note B(800).
| Vidéo sur l’utilisation d’une demi-droite graduée |
III – Comparaison et rangement
- Ranger des nombres dans l’ordre croissant signifie les ranger du plus petit au plus grand.
- Ranger des nombres dans l’ordre décroissant signifie les ranger du plus grand au plus petit.
Exemple : Pour ranger les nombres 25 342 ; 253 420 ; 25 243 ; 235 420 ; 25 324 dans l’ordre croissant, on repère le plus petit, puis le plus petit des nombres qui restent, et ainsi de suite jusqu’au dernier.
On obtient donc : 25 243 – 25 324 – 25 342 – 235 420 – 253 420.
IV – Addition
- Les nombres que l’on additionne s’appellent les termes.
- Le résultat d’une addition s’appelle la somme.
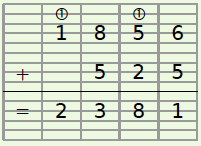Exemple : On pose et on calcule : 1 856 + 525.
On place les chiffres les uns sous les autres en commençant par les chiffres des unités.
- Les nombres 1 856 et 525 sont les termes de l’addition.
- Le résultat 2 381 est la somme.
Dans une addition, on a le droit de :
- regrouper les termes ;
- changer des termes de place.
Exemple : Comment calculer astucieusement 46 + 37 + 54 + 63 ?
46 + 37 + 54 + 63 = (46 + 54) + (37 + 63) = 100 + 100 = 200
V – Soustraction
- Les nombres que l’on soustrait s’appellent les termes.
- Le résultat d’une soustraction s’appelle la différence.
Exemple : On pose et on calcule : 233 − 67.
On procède comme pour l’addition.
- Les nombres 233 et 67 sont les termes de la soustraction.
- Le résultat 166 est la différence.
VI – Chiffres romains
Les 10 chiffres que nous utilisons pour écrire des nombres ont été inventés par les indiens et transmis en Europe par l’intermédiaire des arabes. Avant leur apparition, les hommes comptaient en utilisant d’autres systèmes plus ou moins complexes, mais bien moins efficaces que notre notation décimale actuelle.
Les romains ont emprunté à leurs voisins du Nord, les Étrusques, leur alphabet et leurs chiffres :
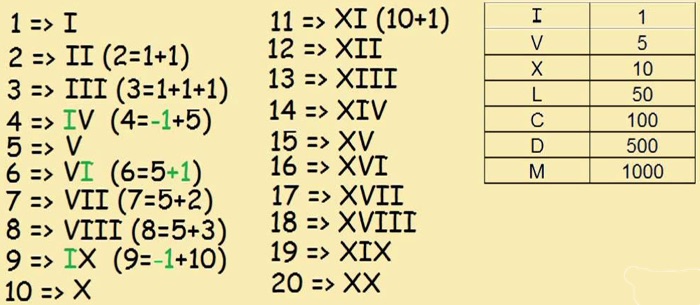
Ainsi, le nombre 123 s’écrivait : CXXIII et l’année 2020 en chiffres romains s’écrit : MMXX.
La grande faiblesse du système romain réside dans l’absence de zéro. Ils ne pouvaient pas utiliser leur système pour faire des opérations. Ils utilisaient pour cela un abaque.
EXERCICES
- 1/8 : Écriture décomposition vers chiffres
- 2/8 : Décomposition
- 4/8 : Écriture en lettres
- 6/8 : Écriture lettre vers chiffres
- 10/8 : Recherche position des chiffres
- 12/8 : Ecriture position vers chiffres
- 14/8 : Devinette
- 15/9 : Suite logique à compléter
- 17/9 : Abscisses de points
- 21/9 : Classement de nombres
- 24/9 : Devinette
- 25/9 : Encadrement
- 28/10 : Ordre de grandeur additions
- 30/10 : Calcul astucieux
- 35/10 : Opérations à trous
- 37/10 : Ordre de grandeur soustractions
- 41/10 : Traduire une opération mots vers nombres
- 46/11 : Date à calculer
- 50/11 : Tour Eiffel
