Les parallélogrammes – Première partie

I – Définition et propriétés

Définition
Un polygone est une figure plane fermée par des segments de droites.

Étymologie grecque : 

  • polus : nombreux
  • gônia : angle
Définition
Un quadrilatère est un polygone à quatre côtés.

Étymologie latine :

  • quatuor : quatre
  • latus : côté
Vocabulaire
Un quadrilatère a quatre sommets, quatre côtés et deux diagonales.

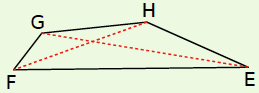Exemple :

  • EFGH est un quadrilatère.
  • Le sommet opposé au sommet E est le sommet G.
  • Un côté consécutif au côté [FG] est le côté [EF] ou le côté [GH].
  • Ses diagonales sont les segments [EG] et [HF].
Définition
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.

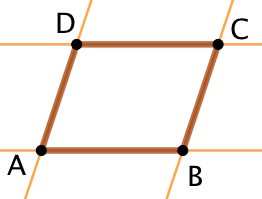Exemple :

  • Les droites (AB) et (CD) sont parallèles.
  • Les droites (AD) et (BC) sont parallèles.
  • Donc ABCD est un parallélogramme.

 

Propriété
Si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur milieu. Ce milieu est le centre de symétrie du parallélogramme.

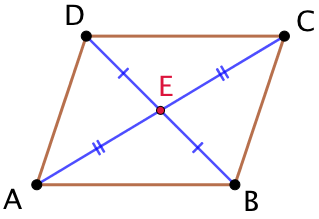Exemple : Soit un parallélogramme ABCD.

  • Ses diagonales [AC] et [BD] se coupent en leur milieu E.
  • E est le centre de symétrie de ABCD.
  • [AB] et [CD] sont symétriques par rapport à E.
  • [AD] et [BC] sont symétriques par rapport à E.

 

Propriété
Si un quadrilatère est un parallélogramme alors :

  • les côtés opposés ont la même longueur.
  • les angles opposés ont la même mesure.

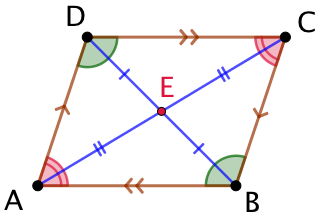Exemple : Soit le parallélogramme ABCD.

  • On sait que les côtés opposés sont symétriques par rapport au milieu des diagonales. Donc ils ont la même longueur.
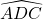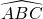  • On sait aussi qu’une symétrie centrale concerne les mesures d’angles. Donc les angles \widehat{ADC} et \widehat{ABC} ont la même mesure, ainsi que les angles 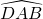\widehat{DAB} et \widehat{DCB}.

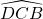II – Savoir reconnaître un parallélogramme

Pour démontrer qu’un quadrilatère est un parallélogramme, on peut revenir à la définition du parallélogramme. Sinon, on peut utiliser l’une des propriétés suivantes sur les quadrilatères.

Propriété
Si un quadrilatère a ses diagonales qui se coupent en leur milieu, alors c’est parallélogramme.

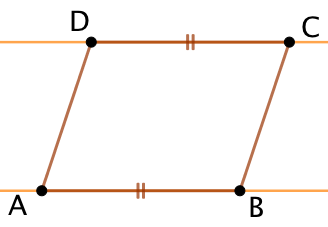
Exemple : Soit ABCD un quadrilatère.

Si on sait que les diagonales [AC] et [BD] de ce quadrilatère se coupent en leur milieu E, alors ABCD est un parallélogramme.

 

Propriété
Si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur, alors c’est parallélogramme.

Exemple : Soit ABCD un quadrilatère.

Si on sait que :

  • les droites (AB) et (CD) sont parallèles ;
  • les longueurs AB et CD sont égales ;
  • les côtés [AB] et [CD] ne se croisent pas ;

Alors ABCD est un parallélogramme.

Propriété
Si un quadrilatère non croisé a ses côtés opposés de même longueur, alors c’est parallélogramme.

Exemple :

Soit ABCD un quadrilatère.

Si on sait que :

  • les longueurs AB et CD sont égales ;
  • les longueurs AD et BC sont égales ;
  • les côtés [AB] et [CD] ne se croisent pas ;

Alors ABCD est un parallélogramme.

Construction d’un parallélogramme

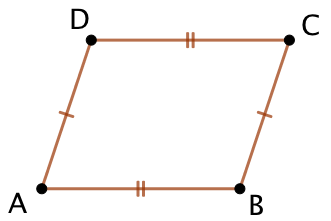
On donne trois points A, B et C. On doit trouver la position du point D telle que ABDC soit un parallélogramme.

On va utiliser la propriété précédente en recherchant un point D tel que BD = AC et CD = AB.
On trace un arc de cercle de centre B et de rayon AC.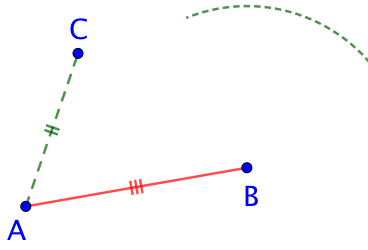
On trace un arc de cercle de centre C et de rayon AB.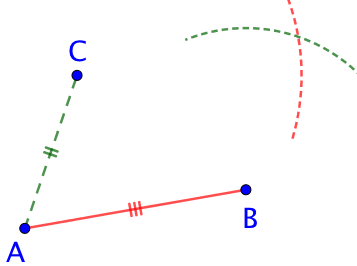
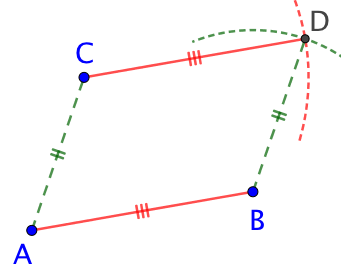
Ces deux arcs de cercle se coupent au point D.

Par construction BD = AC et CD = AB. Donc ABDC est un quadrilatère non croisé dont les côtés opposés sont de même longueur. C’est un parallélogramme.
Print Friendly, PDF & Email