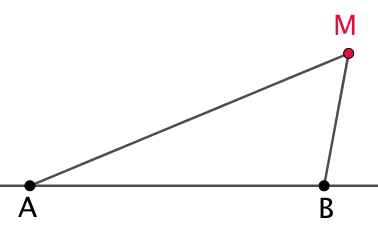
Étant donnés deux points A et B et un réel ![]() , le lieu des points M tels que
, le lieu des points M tels que ![]() est un cercle.
est un cercle.
 |
 |
 |
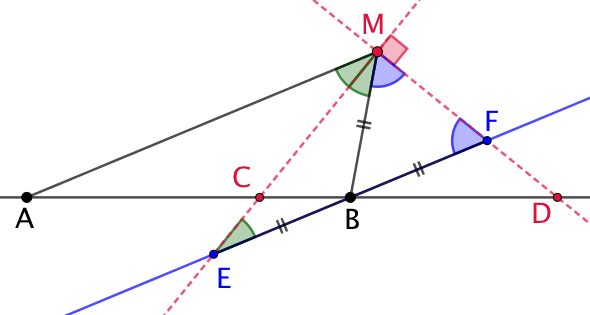
| Soit M l’un des points recherchés. Alors |
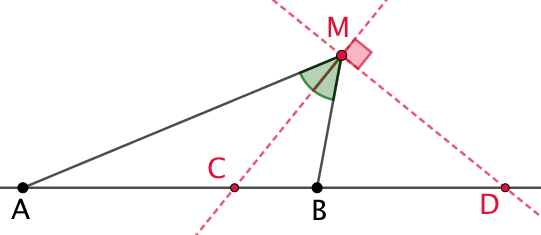
On trace les deux bissectrices de l’angle |
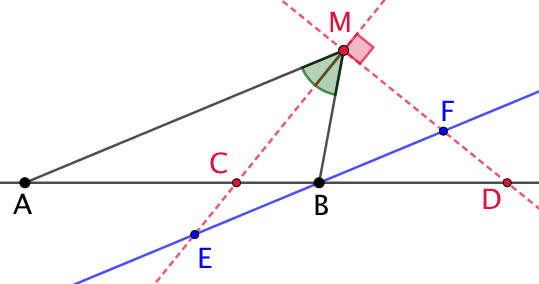
On trace la droite parallèle à (AM) passant par B. Celle-ci coupe les bissectrices en E et F. |
 |
 |
 |
| (AM) et (EF) sont parallèles donc la sécante (EM) crée deux angles |
On note que |
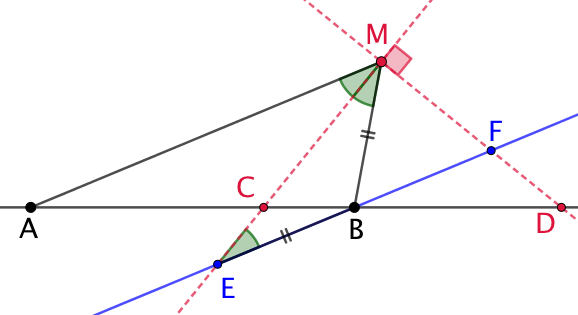
Le théorème de Thales sur ACEBM : Le théorème de Thales sur ADM : Comme |
Donc les positions des points C et D ne dépendent que des points A et B et de la valeur de ![]() . Elles ne dépendent pas du point M. Par ailleurs
. Elles ne dépendent pas du point M. Par ailleurs ![]() est par construction un angle droit.
est par construction un angle droit.
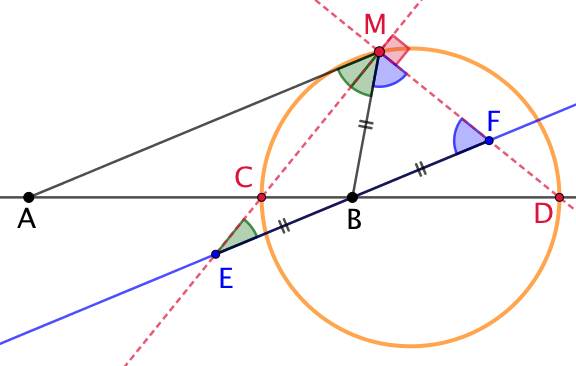
Conclusion : les points M recherchés voient un segment donné [CB] sous un angle de mesure constante ![]() . Le lieu recherché est le cercle de diamètre [CD] passant par C et D.
. Le lieu recherché est le cercle de diamètre [CD] passant par C et D.
Voir aussi : Bissectrices et division harmonique
