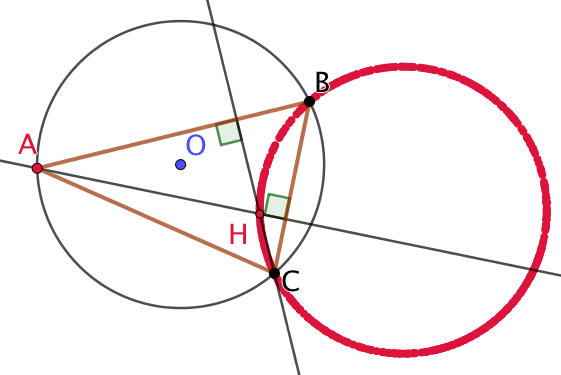
Etant donnés un cercle et deux points B et C sur ce cercle, un point A mobile sur ce cercle. Le lieu géométrique de l’orthocentre du triangle ABC est un second cercle, le symétrique par rapport à (BC) du premier cercle.
Explications :
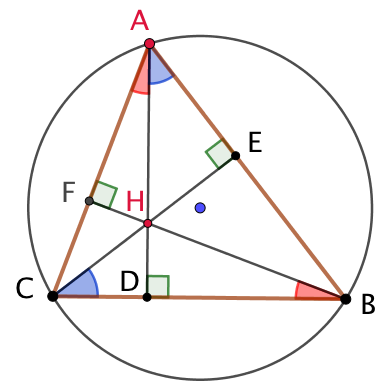
Soit H l’orthocentre de ABC. On va montrer que la mesure de l’angle 
est indépendante de la position de H. Cela démontrera que lorsque A se déplace, les différentes positions de H sont cocycliques avec les points B et C.
.
. Or 
car ces angles ont deux côtés deux à deux perpendiculaires.
et 
. Or 
car ces angles ont deux côtés deux à deux perpendiculaires.
Alors 
Il reste à déterminer les paramètres de ce cercle passant par A et B.
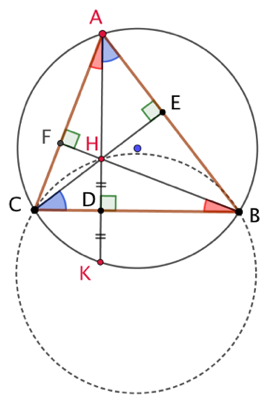
Soit K le symétrique de l’orthocentre H par rapport à (BC). On sait que K appartient au cercle circonscrit à ABC. Lorsque A parcourt le cercle, K parcours aussi le même cercle. Alors nécessairement H, symétrique de K, parcourt un cercle symétrique de notre cercle de départ, de même rayon et dont le centre est le symétrique axial du cercle de départ par rapport à (BC).
Voir : Symétrique axial de l’orthocentre
