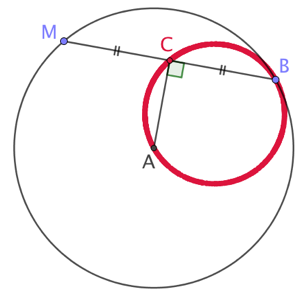
 Étant donné un cercle de centre A et un point B fixe sur ce cercle, quel est le lieu géométrique des milieux de toutes les cordes passant par ce point ?
Étant donné un cercle de centre A et un point B fixe sur ce cercle, quel est le lieu géométrique des milieux de toutes les cordes passant par ce point ?
Réponse : c’est un cercle passant par A et B, et de diamètre AB.
Explications :
Soient un cercle de centre A, un point B fixe de ce cercle, un point M mobile sur ce cercle et C le milieu du segment [MB].
Par conséquent la droite (AC) est la médiatrice du segment [MB]. Quand M parcourt le cercle de centre A, C décrit une certaine figure tel que le triangle ABC reste rectangle en C. Donc C appartient au cercle de diamètre AB passant par A et B.
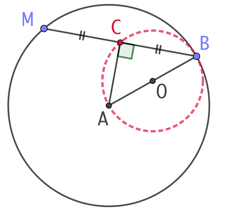 Inversement, soit C un point du cercle de centre O, milieu du segment [AB] et de diamètre AB. Alors ABC est un triangle rectangle. Donc les droites (CA) et (CB) sont perpendiculaires.
Inversement, soit C un point du cercle de centre O, milieu du segment [AB] et de diamètre AB. Alors ABC est un triangle rectangle. Donc les droites (CA) et (CB) sont perpendiculaires.
Soit M le point d’intersection de la droite (BC) avec le cercle de centre A passant par B. Donc les droites (MB) et (CA) sont perpendiculaires. Alors C est le milieu de la corde [MB].
