Soient deux droites 
et 
sécantes en A. Le lieu des points dont la différence des distances à et à est constante et égale à 
est constitué de huit demi-droites.
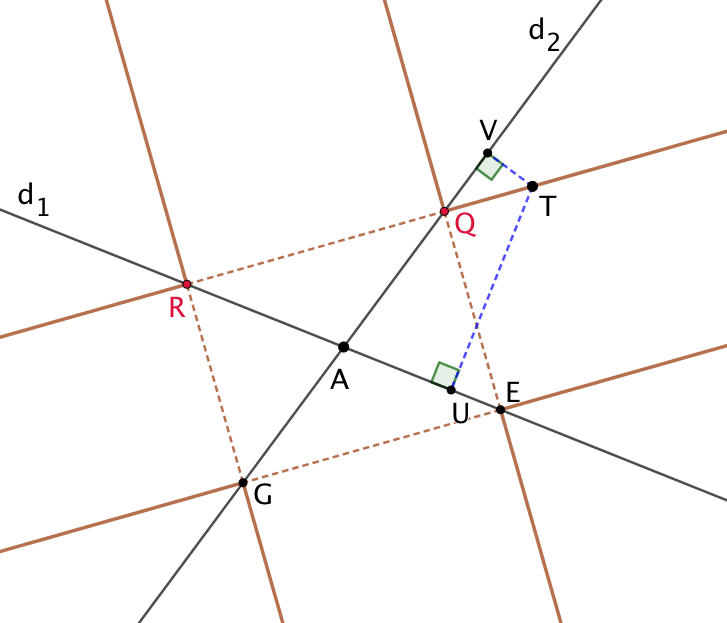
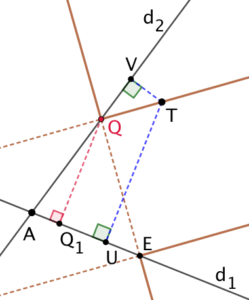
Ces 8 demie-droites sont construites à partir des 4 droites (RQ), (QE), (EG) et (GR) dont on aurait retiré les 4 côtés du rectangles RQEG.
Par exemple le point Q de la droite (d_2) tel que sa distance à (d_1) est 
est un point limite du lieu géométrique.
T est un point de ce lieu car 
.
Pour comprendre, voir : Lieux géométrique des points dont la somme des distances à deux droites est constant
