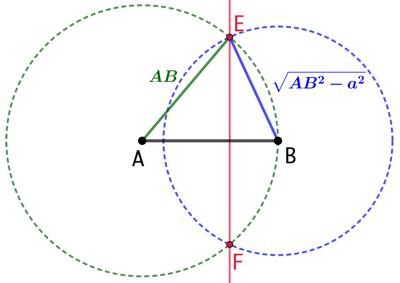
Étant donnés un segment [AB] et un nombre réel a, le lieux des points M tels que ![]() est une droite perpendiculaire à (AB).
est une droite perpendiculaire à (AB).
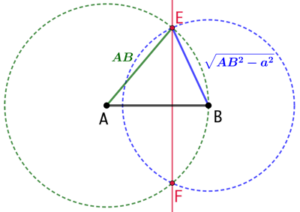 Construction :
Construction :
L’égalité ![]() peut s’interpréter comme décrivant la position d’un point situé à l’intersection de deux cercles dont les carrés des rayons ont une différence de
peut s’interpréter comme décrivant la position d’un point situé à l’intersection de deux cercles dont les carrés des rayons ont une différence de ![]() .
.
Pour trouver deux de ces points :
- On trace le cercle de centre A et de rayon AB;
- On trace le cercle de centre B et de rayon
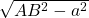 ;
; - Les points d’intersection E et F de ces deux cercles définissent la droite (EF) qui est le lieu recherché.
 Explications :
Explications :
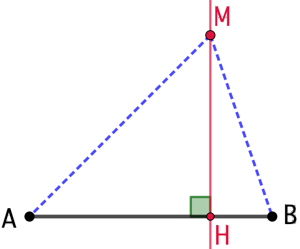
Soient M un point tel que ![]() et H la projection de M sur la droite (AB). On va déterminer une expression de la distance AH.
et H la projection de M sur la droite (AB). On va déterminer une expression de la distance AH.
On utilise le théorème de Pythagore pour trouver deux expressions de MH :
![]() et
et ![]() , ce qui donne l’équation :
, ce qui donne l’équation : ![]() , que l’on peut écrire ainsi :
, que l’on peut écrire ainsi : ![]() , soit
, soit ![]() .
.
Après factorisation et en rappelant que ![]() , on obtient
, on obtient ![]() .
.
En posant ![]() , on arrive à
, on arrive à ![]() , soit
, soit ![]() .
.
Ainsi le lieu recherché est la droite perpendiculaire à (AB) passant par le point H.
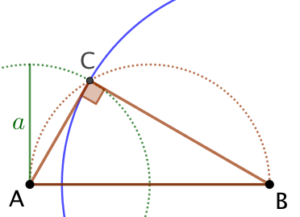 Remarque : Méthode pour tracer un cercle de rayon
Remarque : Méthode pour tracer un cercle de rayon ![]() et de centre B.
et de centre B.
- On trace un cercle de diamètre AB passant par A et B.
- On trace un cercle de centre A et de rayon
 .
. - Soit C, le point d’intersection des deux cercles.
- Le cercle de centre B et passant par C est le cercle recherché.
En effet : Par construction ABC est rectangle en C. Donc ![]() . Ainsi
. Ainsi ![]()