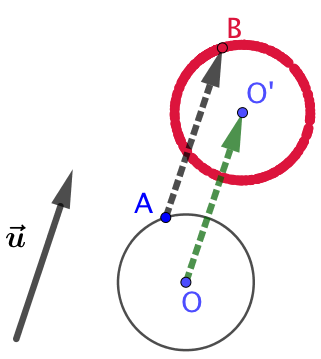
L’image d’un cercle de centre O par une translation de vecteur 
est le cercle de même rayon et de centre O’ image de O par la translation.
Explications :
Soit un point quelconque A du cercle de centre O et A’ son image par la translation de vecteur . Alors 
.
Comme 
il vient que 
. Donc AOO’B est un parallélogramme. Ce qui permet d’affirmer que OA = O’B et que B est sur le cercle de centre O’ et de rayon OA.
On vient de démontrer que l’image du cercle de centre O est contenue dans un cercle de centre O’ et de même rayon. On démontre très facilement que tout point du cercle de centre O’ est l’image d’un point du cercle de centre O.
