Médianes d’un triangle

La médiane issue d’un sommet d’un triangle est la droite joignant ce sommet au milieu du côté opposé à ce sommet.

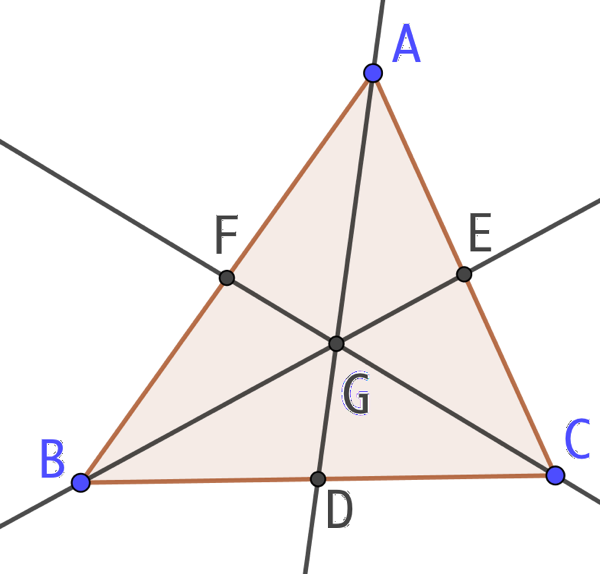
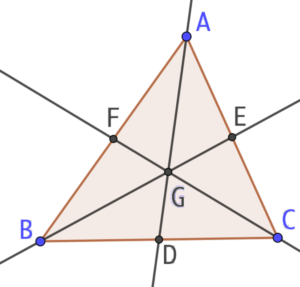
1. On construit les trois médianes du triangle ABC
2. On observe que ces médianes sont concourantes en un point G appelé le centre de gravité du triangle.

Explications n°1 :

Soit G le point d’intersection des médianes (CF) et (AD). On démontrer que G appartient à la médiane (BE).

G est sur la médiane (CF) donc : . Voir : point sur une médiane

G est sur la médiane (AD) donc : . Par conséquent : . Ce qui permet d’affirmer que G appartient aussi à la médiatrice (BE).

Explications n°2 :

Soit G le point d’intersection des médianes (CF) et (AD). On place H le symétrique de B par rapport à G. La droite (BH) coupe (AC) en E. On va démontrer que E est le milieu du segment [AC].

Si (AD) est la médiane issue de A alors D est le milieu de [BC]. Si H est le symétrique de B par rapport à G alors G est le milieu de [BH].

On applique le théorème des milieux au triangle BCH; ce qui permet d’affirmer que (GD) // (HC) et par conséquent que (AG) // (HC).

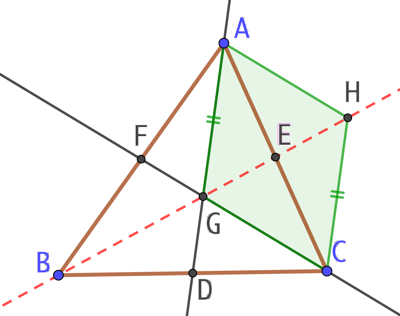
Si (CF) est la médiane issue de C alors F est le milieu de [AB]. On applique le théorème des milieux au triangle ABH;

Ce qui permet d’affirmer que (GF) // (HA) et par conséquent que (CG) // (HA).

Si (AG) // (HC) et (CG) // (HA) alors AGCH est un parallélogramme. Ses diagonales se coupent en leur milieu donc E est le milieu de [AC], ce qui démontre que (BE) est la médiane issue de B et que les trois médianes sont concourantes en G.

Le double usage fait du théorème des milieux permet d’affirmer que . donc puisque AGCH est un parallélogramme. Par conséquent . On démontre de la même façon que et que .