Les médiatrices d’un triangle sont concourantes.
Explications :
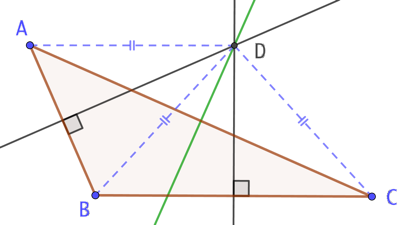
Soit ABC un triangle quelconque. Nommons D l’intersection des médiatrices des segments [AB] et [BC] et démontrons que D appartient à la médiatrice de [AC].
SI D appartient à la médiatrice de [AB] alors DA = DB. Si D appartient la médiatrice de [BC] alors DB = DC. Donc DA = DC et il vient que D appartient à la médiatrice de [AC]. Conclusion : Les médiatrices de ABC sont concourantes en D.
Remarques :
- D est le centre du cercle circonscrit au triangle ABC.
- On a supposé que les médiatrices de [AB] et [BC] étaient sécantes. Si ces droites étaient parallèles alors il en serait de même des droites (AB) et (BC), ce qui est impossible.
