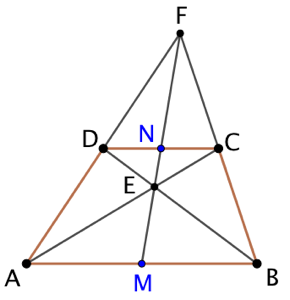
Milieux des côtés parallèles d’un trapèze

Soient ABCD est un trapèze de bases [AB] et [CD], E le point d’intersection des diagonales (AC) et (BD), F le point d’intersection de (AD) et (BC). (FE) croise (AB) en M et (CD) en N. Alors M est le milieu de [AB] et N le milieu de [CD].

Explications : On va démontrer que les triangles EAM et EMB ont la même aire.

(DC) et (AB) étant parallèles:

  • Aire_{AED} = Aire_{BCE}
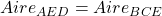
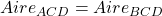  • Aire_{ACD} = Aire_{BCD}. On ajoute à chacun d’eux l’aire de FDC, il vient : Aire_{ACF} = Aire_{BFD}.

    \[ \text{Par ailleurs : } \qquad \qquad \dfrac{Aire_{AED}}{Aire_{ACD}} = \dfrac{AE}{AC} = \dfrac{Aire_{AEF}}{Aire_{ACF}} \qquad \qquad \dfrac{Aire_{BCE}}{Aire_{BCD}} = \dfrac{BE}{BD} = \dfrac{Aire_{BFE}}{Aire_{BFD}} \]

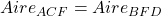\dfrac{Aire_{AED}}{Aire_{ACD}} = \dfrac{Aire_{BCE}}{Aire_{BCD}} donc \dfrac{Aire_{AEF}}{Aire_{ACF}} = \dfrac{Aire_{BFE}}{Aire_{BFD}}.

Aire_{ACF} = Aire_{BFD} donc Aire_{AEF} = Aire_{BFE}. Ce qui permet de conclure que E est sur la médiane de [AB], puis que M est le milieu de [AB].

Le théorème de Thales permet de montrer ensuite que N est le milieu de [DC].

 

 

 

 

 

Print Friendly, PDF & Email