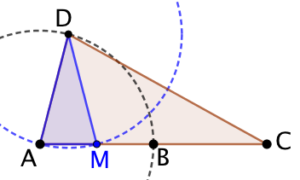
On veut construire le milieu d’un segment [AB] au compas seul. Pour cela on s’appuie sur la construction suivante ci-contre :
C est le symétrique de A par rapport B. CAB est un triangle isocèle en C tel que 
. DAM est un triangle isocèle en D tel que M soit sur (AB). D’après la propriété sur deux triangles isocèles et semblables, nous savons que DAM et CAD sont semblables.
Par conséquent : 
. Ce qui donne : 
. Donc M est le milieu de [AB].
Il suffit de reproduire cette construction au compas seul pour obtenir M :
 |
 |
 |
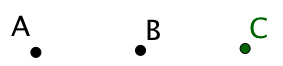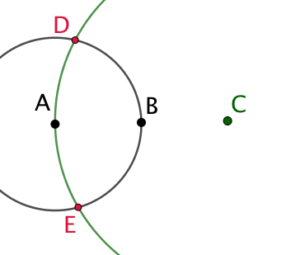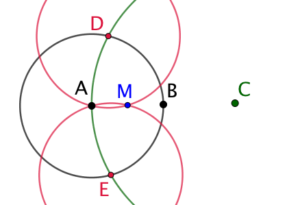| On construit au compas seulement le point C symétrique de A par rapport à B. | On trace le cercle de centre C qui passe par A et le cercle de centre A et qui passe par B. Ainsi on obtient un triangle ACD isocèle en C tel que  . Les intersections de ces deux cercles sont D et E. |
On trace les cercles de centre D et E qui passent par A. La deuxième intersection de ces deux cercles est M, milieu de [AB]. |
 |
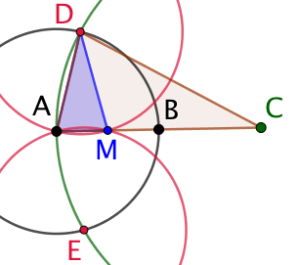Explications : Comme A et M sont le cercle de centre D, DAM est un triangle isocèle. On sait d’après le début de cet article que DAM et CAD sont semblables et que compte tenu de leurs dimensions particulières,  . |
|
